꺼내먹는지식 준
법선벡터를 이용한 직선의 방정식 본문
점 $A(x_1, y_1)$를 지나고 법선벡터가 $\vec{n} = (n_1, n_2)$인 직선의 방정식은
$n_1(x- x_1) + n_2(y-y_1) = 0$
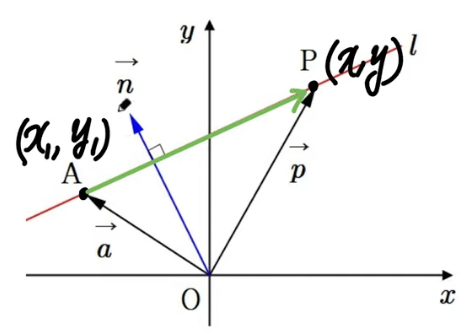
법선 벡터는 내적하면 0 이라는 특성을 이용한 공식이다.
점 - 점 = 벡터 성질을 활용하여
(점 - 점) $\cdot$ 법선 벡터 = 0
로 구했다.
※ 2개의 점을 알아도 직선을 구할 수 있다.
$a_1 x_1 + a_2 x_2 = b$
$Ax = b$
$Ax - b = 0$
'AI > AI 수학' 카테고리의 다른 글
| 초평면이 법선벡터의 곱셈인 이유 (0) | 2022.11.10 |
|---|---|
| 초평면 (0) | 2022.11.08 |
| 벡터의 외적 (1) | 2022.11.04 |
| 아핀 공간 (0) | 2022.11.04 |
| 정규분포 확률밀도함수 유도 (0) | 2022.09.15 |
Comments



