꺼내먹는지식 준
초평면 본문
초평면
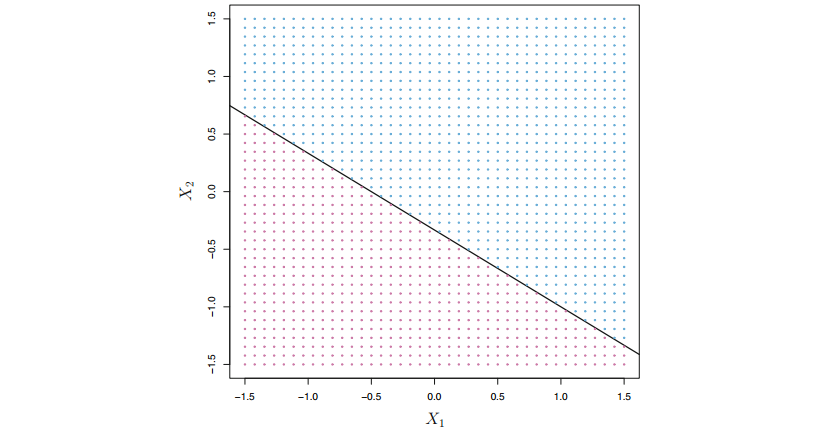
초평면 $1 + 2X_1 + 3X_2 = 0$. $1 + 2X_1 = 3X_2 > 0$은 파란 점이 모인 파란 공간이고 $1+2X_1+3X_2 < 0$ 은 보라색 점이 모인 보라색 공간이다.
p차원 공간에서, 초평면은 p-1 차원인 평평한 아핀 부분 공간이다. 아핀공간에 대한 사전지식이 없는 분은 글을 읽고 오면 좋다.
예를 들어, 2차원 공간에서 초평면은 평평한 1차원 부분공간으로 선이다. 3차원 초평면은 평평한 2차원 부분공간이며 이는 평면이다. p>3 인 경우에는 초평면을 시각화하기 어렵지만 p-1 차원인 평평한 부분 공간인 것은 여전히 유효하다.
2차원에서 초평면의 수학적인 정의는 다음의 방정식으로 정의한다.
$$\beta_0 + \beta_1 X_1 + \beta_2 X_2 = 0$$
2차원의 초평면은 1차원 선이다. 2차원 파라미터 $\beta_0, \beta_1, \beta_2$ 가 존재하며, $X_1, X_2$ 는 초평면 상 임의의 점이다.
위 식은 임의의 p차원으로 확장 할 수 있다. 즉 p차원에 대한 초평면은 아래의 식으로 정의한다.
$$\beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... +\beta_p X_p= 0$$
p차원 공간의 점 $X_1 X_p$가 위 식을 만족하면 X는 초평면 상에 있다.
X가 아래 식을 만족하면 X는 초평면의 한쪽에 놓인 다는 것을 의미한다.
$$\beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... +\beta_p X_p > 0$$
반면 아래 식을 만족하면 X는 초평면의 다른 한쪽에 놓인다.
$$\beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... +\beta_p X_p < 0$$
따라서 초평면은 p차원 공간을 두개로 분할한다고 생각할 수 있다. X가 분리된 두 공간 중 어느 부분에 속하는지 판별하려면 초평면 식에 X를 대힙하여 0보다 큰지 작은지 확인하면 된다.
분리 초평면을 이용한 분류 (Classification Using a Separating Hyperplane)
$p$차원 공간에서 $n$개의 학습 관측값들로 구성된 $n \times p$ 크기의 행렬 $X$가 있다고 가정해보자. 그리고 이 관측값들은 두 개의 class에 속한다. $y_1 \sim y_n$이 -1 또는 1 이다. 목적은학습 셋에 기반한 test observation을 정확하게 분류하는 분류기를 만드는 것이다. 이 분류기를 분리 초평면의 개념으로 만든다.

Training observation이 정답 class label에 해당하도록 완벽하게 분리하는 초평면을 정의할 수 있다고 가정해보자. 위 그림에서 왼쪽 그림은 3개의 분리 초평면 예이다. 분리 초평면을 정의하고 식에 X를 대입했을 때, 0보다 큰지 작은지 판별하여 class를 할당할 수 있다.
$$\beta_0 + \beta_1 x_i1 + \beta_2 x_i2 + ... +\beta_p x_ip > 0 \textrm{ if } y_i = 1,$$
$$\beta_0 + \beta_1 x_i1 + \beta_2 x_i2 + ... +\beta_p x_ip < 0 \textrm{ if } y_i = -1,$$
이를 다르게 표현하면 분리 초평면은 모든 관측값에 대하여 아래의 식을 만족한다.
$$y_i(\beta_0 + \beta_1 x_i1 + \beta_2 x_i2 + ... +\beta_p x_ip) > 0$$
분리 초평면이 존재한다면 이것을 사용하여 자연스러운 분류기를 구성할 수 있다. test observation이 초평면의 어느 면에 위치해있는지에 따라 class를 부여하면 된다. 예를 들어 f(x)가 양수이면 x는 1에 할당, 음수이면 x = -1 에 할당한다.
f(x)의 크기도 활용하여 f(x)가 0과 멀면 x는 초평면과 많이 떨어져 있고 class를 신뢰할 수 있다. 하지만 초평면과 가까우면 클래스에 대한 확신이 덜하다.
'AI > AI 수학' 카테고리의 다른 글
| 초평면이 법선벡터의 곱셈인 이유 (0) | 2022.11.10 |
|---|---|
| 법선벡터를 이용한 직선의 방정식 (0) | 2022.11.09 |
| 벡터의 외적 (1) | 2022.11.04 |
| 아핀 공간 (0) | 2022.11.04 |
| 정규분포 확률밀도함수 유도 (0) | 2022.09.15 |



