꺼내먹는지식 준
아핀 공간 본문
들어가며
벡터는 위치를 가지지 않는다.
위치와 상관 없이 동일한 크기와 방향을 가지는 벡터는 같다.
즉, 기하학에서 벡터는 '방향'과 '변화' 두가지 의미로 사용될 수 있다.
벡터의 덧셈 뺄셈

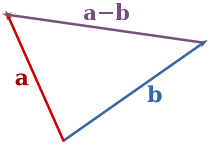
화살표의 방향을 유의해서 보자
벡터의 덧셈의 대수학적 법칙은 실수의 덧셈과 유사하다. 이는 위치를 갖지 않는다는 특성으로 인한다.
1. v + w = w + v (교환법칙)
2. u + (v+w) = (u+v) +w (결합법칙)
3. v + 0 = v (덧셈의 항등원)
4. 모든 v에 대해 v+(-v) = 0 을 만족하는 벡터 -v 가 존재한다. (덧셈의 역원)
뺄셈의 결과 벡터는 두번째 벡터의 머리에서 첫번째 벡터의 머리로 이어진다.
※ 아핀 공간:
한 6년전 그래픽스 논문을 읽다가 도대체 아핀 공간이 무엇인가! 하고 찾아봤던 기억이 있다. 당시에는 지금처럼 한국에 좋은 자료가 많지 않아서 아핀 공간을 잘 이해하기가 어려웠는데, 요새는 좋은 자료가 많다.
일반적으로 유클리드 공간은 아핀 공간이지만 벡터 공간이라고도 한다.
아핀 공간의 정의 자체가 벡터공간을 필요로하기 때문이다.
아핀 공간으로 벡터 공간을 형성할 수 있다고 알고 이해하면 된다고 한다.
일반적으로 직교좌표계에서 점은 원점으로부터 각 축에 대해서 얼만큼 떨어져 있는가 표현된다.

이렇게 정의된 점이 아핀 공간에 있다고 한다.
아핀 공간을 벡터공간이라고만 알기보다는 좀 더 정확히 정의해보자.
V라는 벡터 공간이 있을 때, 이 V 위에서 아핀 공간은 A라는 점들의 집합으로 정의된다.
※ 벡터 공간과 아핀 공간에 대한 직관적인 차이점
아핀 공간과 벡터 공간의 차이점
아핀 공간과 벡터 공간의 차이점은 무엇일까? 먼저 벡터를 표현할 때는 기본 과정이 존재한다. 벡터는 그림 1과 같이 원점을 기준으로 방향과 크기를 나타낸 것이다. 하지만 그림 2에서는 원점에
gyong0.tistory.com
$$A \times V \rightarrow A$$
$$P,v | \rightarrow P+v$$
($P$는 $A$ 공간의 점, $v$는 $V$에 속한 임의의 벡터)
$V$와 $A$ 사이에는 위 2가지 두 대응이 존재한다고 한다.
※ 점과 벡터가 + 연산이 되는이유
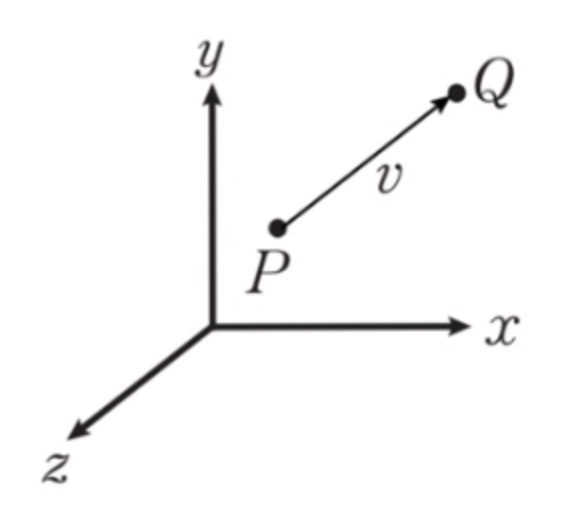
$P$(점)에서 $v$(벡터)를 더해서 $Q$(점)이 나오는 것
$$P = (p_x, p_y, p_z)$$
$$v = (v_x, v_y, v_z)$$
$$Q = P + v $$
$$ = (p_x, p_y, p_z) + (v_x, v_y, v_z)$$
$$= (p_x + v_x, p_y + v_y, p_z + v_z)$$
즉, 아핀 공간에서 덧셈 연산을 할 때는
벡터와 벡터의 연산인지, 점과 벡터의 연산인지에 유의해서 정확하게 봐야한다.
또한 3가지 성질이 있다.
1. $A$에 속한 모든 점 $P$에 대해서 $P + \vec{0} = P$ 이다. 영 벡터$(\vec{0})$는 벡터 공간 $V$의 항등원이다.
2. $A$에 속한 모든 점 $P$와 $V$에 속한 임의의 벡터 $v,w$에 대해 $P + (v + w) = (P+v)+w$ 가 성립한다.
3. $A$에 속한 점 $P,Q$가 있을 때 $P + v = Q$를 만족하는 단 하나의 벡터 $v$가 존재한다.
3번이 좀 헷갈리니 살펴보자. 점 2개를 찍어놓고 두 점 사이에 존재하는 벡터는 하나라는 것을 쉽게 확인할 수 있다. (방향 크기 동일)
즉 이에 따라 $Q-P = v$ 점 $Q$ 에서 점 $P$를 빼면 벡터 $v$를 얻는다는 것을 알 수 있다.
벡터와 벡터의 연산은 벡터
벡터와 점의 연산 점
점과 점의 뺄셈 연산 벡터
위의 조건을 만족하는 공간이 바로 아핀 공간이다.
점 다음으로 선을 살펴보자.
2차원에서 선을 표현하는 것은 가능하지만, 3차원에서 선을 표현하는 것이 불가능하다.
실제로 불가능하다기 보다는 $ax + by + c = 0$ 형태로 표현이 불가능하다.
성분이 늘어나기에 사실상 평면의 방정식이 되어버린다.
이에 따라 3차원에서는 매개변수 방정식(parameteric equation)을 통해 선을 표현한다.

어떤 방향벡터와 점이 선을 표현할 수 있게 된다.
위 방향벡터는 점과 점을 뺀 결과이다.
t는 음의 무한대~ 양의 무한대의 실수 범위를 가지고 있다.
$$L(t) = P + t \cdot v $$
$$= P + t \cdot(Q - P)$$
$$= P + t \cdot Q - t\cdot P$$
$$= (1-t) \cdot P - t \cdot Q$$
위와 같이 직선을 표현하는 과정에서 $(1-t)$ 와 $t$ 를 주목하며 봐보자.
점에다가 스칼라를 곱하고 이를 더한다.
아핀 공간에서 점과 점의 덧셈은 안되는 줄만 알았는데 벡터 공간의 선형 조합처럼 아핀 조합이라는 것이 존재한다.
※ 벡터공간의 선형 조합
$ <v_1, ... v_n> = \{ a_1 v_1 + ... + a_n v_n | a_i \in F \}$
벡터들에 스칼라배를 해서 더함으로서 수많은 벡터를 만들 수 있고, 이를 통해 공간 자체를 span 할 수 있다는 뜻
선형 조합들이 벡터들에게 임의의 스칼라 값을 곱해서 새로운 벡터를 만든다면,
아핀 조합은 점들에게 특정 조건을 만족하는 스칼라 값을 곱해서 더하면 새로운 점이 나온다.
다만, 벡터는 임의의 스칼라지만, 점은 특정 스칼라의 곱이다.
아핀 조합은 점과 벡터의 덧셈연산에서 나온다.
점에다 벡터를 더하면 아래와 같다.
$$P = P_0 + v $$
$$P = P_0 + (a_1 \cdot v_1 + ... + a_n \cdot v_n)$$
쉽게 생각하기 위해서
P0가 중심이라고 생각하면
$v_1 \sim v_n$ 은 기저벡터라고 볼 수 있다.
그리고 기저벡터는 다시 아래와 같이 다르게 표현할 수 있다.
점 - 점 = 벡터
$$v_1 = P_1 - P_0$$
$$v_1 = P_2 - P_0$$
$$v_1 = P_3 - P_0$$
$$\cdots$$
$$v_i = P_i - P_0$$
위 결과를 통해 아래와 같이 정리할 수 있다.
$$P = P_0 + (a_1 \cdot v_1 + \cdots + a_n \cdot v_n)$$
$$P = P_0 + a_1 \cdot (P_1 - P_0) + a_2 \cdot (P_2 - P_0) + \cdots + a_n \cdot (P_n - P_0)$$
$$P = (1 - a_1 - a_2 - a_3 - \cdots - a_n) \cdot P_0 + a_1 \cdot P_1 + a_2 \cdot P_2 + \cdots + a_n \cdot P_n$$
위 식이 바로 새로운 점을 만드는 아핀 조합이다.
각 스칼라값만 뽑아보면 아래와 같이 된다.
$$(1 - a_1 - a_2 - a_3 - \cdots - a_n) + a_1 + a_2 + a_3 + \cdots a_n = 1$$
아핀 조합의 스칼라 조건
모든 점에 대해서 스칼라 값의 합이 1이 된다.
기저벡터들의 조합으로 벡터공간이 형성되듯이 $P_0 ~ P_n$ 점들의 조합으로 아핀 공간이 생긴다.
아핀 조합에 참여한 점들은 임의의 점이 아니라 서로 아핀 독립(affinely independent)하다.
아핀 독립이란 쉽게 말해서 점 집합에서 임의의 한 점이 나머지 점들을 아무리 아핀 조합을 한들 만들어질 수 없다는 것을 의미한다.
(기저벡터와 유사 y 와 x 벡터를 아무리 조합해도 x 벡터를 만들 수는 없다. )
각 점들이 아핀독립인지 확인하는 방법은 벡터를 이용하는 방법이다.
정렬된 점들이 서로에게 아핀 독립이면 이 점들을 차례대로 두 개씩 골라서 만들어지는 벡터 또한 선형 독립이 되는 것을 이용한다.
이 벡터들이 한 벡터 공간의 기저 벡터가 된다는 점을 이용하는 것이다.
아핀 독립인 점들의 집합을 단체, simplex 라고 하고, 아핀 조합에 등장하는 스칼라값들을 아핀 조합으로 생성되는 점의 무게중심좌표, barycecntric coordinate이라고 한다.
위에서 살펴보았던 매개변수 방정식은 아핀 조합임을 알 수 있다.
$$L(t) = P + t \cdot v $$
$$= P + t \cdot(Q - P)$$
$$= P + t \cdot Q - t\cdot P$$
$$= (1-t) \cdot P - t \cdot Q$$
PQ 벡터는 유일한 기저벡터가 된다.
이 아핀 조합은 1차원 아핀 공간을 생성하고 이것이 바로 선이 되는 것이다.
직선이 아니라 선분을 표현하고 싶다면 t 값의 범위를 정해주면 선분이 된다.
예를 들어 t = [0, 1] 범위라면 P 와 Q를 잇는 선분이 만들어질 것이다.
점, 선 다음으로 면을 알아보자.
선을 만들 때 두점의 아핀 조합을 통해 만들었다.
면을 만들 때는 세점의 아핀 조합을 통해서 만든다.
면도 매개변수 방정식으로 표현된다.
한 평면에 점 3개 A,B,C 가 있다면 아래와 같이 표현할 수 있다.
$$P(s,t) = (1 - s - t) \cdot A + s \cdot B + t \cdot C$$
$$= A + s \cdot (B - A) + t \cdot (C - A)$$
$$= A + s \cdot u + t \cdot v$$ (햇갈리니 벡터는 벡터표시를 해주자)
$$= A + s \cdot \vec{u} + t \cdot \vec{v}$$
점과 점의 뺄샘 계산으로 벡터를 만들어서 점 하나와 2개의 벡터 계산으로 바꿀 수 있다.
3차원 공간에서 선을 표현할 때는 매개변수 방정식으로 많이 표현하지만,
3차원 공간에서 면을 표현할 때는 매개변수 방정식과 함께 일반화 표현을 많이 사용한다.
(3D 게임에서 평면을 다룰 때는 매개변수보다 일반화 방정식이 더 이해하기 수월하다.)
고등학교에서는 한 점과 법선벡터가 주어졌을 때 평면을 모두 만들 수 있다고 배웠다.
한 점 : P, 법선벡터: n
$$P = (p_x, p_y, p_z)$$
$$n = (a,b,c)$$
임의의 평면의 점 Q에 대해서 성립해야 그것이 평면이다.
$$Q = (x,y,z)$$
$$v = Q - P$$
$$v = (x - p_x, y - p_y, z - p_z)$$

어떤 Q를 잡아도 그 벡터와 법선벡터를 내적하면 0이 나와야 한다.
$n \cdot v = 0$
$(a,b,c) \cdot (x - p_x, y - p_y, z - p_z) = 0$
$a \cdot (x - p_x) + b \cdot (y - p_y) + c \cdot (z - p_z)$
$a \cdot x + b \cdot y + c \cdot z - (a \cdot p_x + b \cdot p_y + c \cdot p_z) = 0$
$a \cdot x + b \cdot y + c \cdot z - n \cdot P = 0$
우리가 알던 평면의 방정식을 얻게 된다.
매개변수가 기하학적으로 해석이 되었다.
여기서 n 과 p 의 내적을 d 로만 고치면 우리가 알던 평면의 방정식을 얻는다.
$$ax + by + cz + d = 0$$
법선 벡터는 단위벡터인게 좋다. 점과 평면 직선거리를 쉽게 구할 수 있기 때문이다.
(정규화 시키려면 크기로 나누면 된다. 나머지 성분들도 변한다는 것 유의 )
평소에 한점과 법선 벡터로 평면의 방정식을 구했다.
그렇다면 세 점으로는 어떻게 평면을 구하는지 알아보자.
간단하게 설명하면 세점으로 2개의 벡터를 만들고 외적을 하면 법선벡터가 나올 것이다.
또 나머지 한점으로 위 과정을 반복하면 된다.
$$v = Q - P$$
$$w = R - P$$
$$n = v \times w = (a,b,c)$$
$$d = -n \cdot P$$
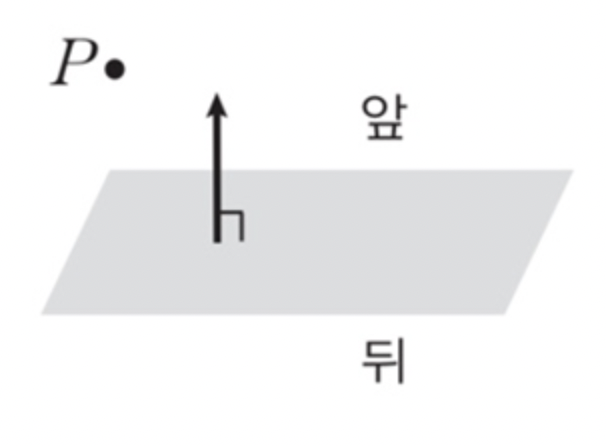
하지만 여기서 법선 벡터가 2개를 얻을 수 있다.
앞으로 나올지, 뒤로 나올지는 외적의 계산 순서에 따른다.
다만, 공간의 임의의 점이 평면의 앞에 있는지 뒤에 있는지를 평면의 방향 기준으로 정하기 때문에 평면의 방향을 중요한 의미가 있다.

다음과 같이 6개의 평면이 닫힌 공간이 있을 때, 법선 벡터의 방향에 따라 겉과 안을 구분하게 된다.
대입을 해보면 수식적으로 앞인지 뒤인지 알수 있다.
$$ax + by + cz + d$$
계산해서 양수가 나오면 앞에 있고
음수가 나오면 뒤에 있다.
당연히 0이 나오면 평면 상에 있다.
매개변수가 아니라 일반화 방정식을 쓰는 이유가 바로 대입하면 어디 있는지 바로 확인할 수 있기 때문이다.
법선 벡터가 단위벡터라면 그 점을 대입한 값에 절대값을 취하면 바로 그 점과 평면 사이의 거리가 된다. (아니면 법선 벡터의 크기만큼 나눠주면 된다.)
임의의 점이 주어졌을 때 같은 평면 상에 존재하는지 구별하는 법을 알았으니 여기서 그만 멈추도록 하자.
점 A, B , C ,D 가 주어졌을 때, 각 점을 이용하여 벡터를 만든다.
$$ u = B - A$$
$$ b = C - A$$
$$ w = D - A$$
4 점이 다 같은 평면상에 있다면 3 개 중 2개의 벡터는 외적하고 그 결과를 나머지 남은 벡터와 내적해서 0이 나오면 그 3개의 벡터는 동일 평면 상에 존재한다고 말 할 수 있다.

마지막으로, 컴퓨터 그래픽스에 많이 사용되는 삼각형에 대해 공부해보자.
아래를 읽기 전에 이 글을 읽고 오면 배경 설정에 도움이 된다.
https://math-development-geometry.tistory.com/44
평면(Plane) 에 대한 이야기
기하학에서 평면은 매우 중요한 요소입니다. 점, 선, 면과 같이 각 차원에서 기본적인 요소가 되는 것들이죠. 이중에서 평면에 대해 이야기를 하도록 하겠습니다. 평면은 평평한 면으로 곡률이
math-development-geometry.tistory.com
사각형은 삼각형 두개로 표현된다. 가장 작은 도형이 삼각형이고, 삼각형 보다 꼭지점이 많은 도형들은 3각형으로 모두 쪼갤 수 있다.
또한 삼각형은 세점이 항상 동일 평면 위에 존재할 수 있는 유일한 도형이다.
(마치 삼각대의 다리 3개가 평면을 만들어 중심을 잡는 것과 같은 맥락이다.)
삼각형에 색을 칠하면 그제서야 우리는 볼 수 있다.
아래 모델을 살펴보자.

선들로 닫혀진 공간이 바로 삼각형이 된다. (주로 polygon 이라 부른다.)
이 폴리곤을 이루는 점을 vertex, 삼각형은 볼록다각형, convex polygon 이라 한다.
※ 볼록 다각형
1. 이어진 두 선분이 이루는 각이 180도 보다는 작거나 같다.
2. 임의의 두 꼭지점을 이은 선은 다각형의 내부에 있거나 다각형을 이루는 선 중에 하나다.

저번에도 평면의 앞 뒤 여부가 중요했듯이,
삼각형도 특정 점이 삼각형 내부에 있는지 외부에 있는지가 중요하다.
A,B,C는 삼각형의 점이고 삼각형 안에 점 D가 있다고 가정하자.
동일 평면상에 있는지는 위에서 4개의 점에 대해 확인하는 법을 배웠다.

다음의 4점으로부터 다시 벡터 6개가 정의된다.
D 중심
$$u_1 = D - A$$
$$u_2 = D - B$$
$$u_3 = D - C$$
반시계 방향
$$v_1 = B - A$$
$$v_2 = C - B$$
$$v_3 = A - C$$
아래는 외적의 결과이다.
$$w_1 = u_1 \times v_1$$
$$w_2 = u_2 \times v_2$$
$$w_3 = u_3 \times v_3$$
만약 점 D 가 삼각형 안에 있다면 외적한 결과값 $w_1, w_2, w_3$ 가 같아진다.
모두 시계방향의 외적 순서이다.
하지만 점 D 가 삼각형 밖에 있다면 외적한 결과값 중 한 벡터의 방향이 반대로 된다.
위 설명은 아래 글로 대체
https://hwanggoon.tistory.com/114
삼각형 안에 점이 있는지 확인하는 방법
삼각형 안에 점이 있는지 확인하는 방법 삼각메쉬 안에 버텍스가 포함되어 있는지는 외적과 내적을 이용하면 확인 할 수 있습니다. 다음 삼각 메쉬에 파란색 점이 밖에 있습니다. ab = A점에서 B
hwanggoon.tistory.com
(외적한 결과는 외적하는 순서에 따라 결정된다. 오른손의 법칙 기억)
외적이 기억나지 않는다면 해당 글을 참고하자.
외적한 결과가 달라지므로 구분할 수가 있게 된다.
즉 아래 조건을 만족하면 벡터의 방향이 모두 같으므로 삼각형 안에 점이 존재한다.
$$w_1 \cdot w_2 > 0$$
$$w_2 \cdot w_3 > 0$$
$$w_3 \cdot w_1 > 0$$
면을 표현할 때는 일반방정식이 더 편리했지만, 삼각형 내부범위 조사는 매개변수가 더 편리하다.
세점으로 식을 유도하자.
$$P(s,t) = (1 - s - t) \cdot A + s \cdot B + t \cdot C$$
$$= A + s \cdot (B - A) + t \cdot (C - A)$$
$$= A + s \cdot u + t \cdot v$$ (햇갈리니 벡터는 벡터표시를 해주자)
$$= A + s \cdot \vec{u} + t \cdot \vec{v}$$
직선의 방정식을 매개변수에 범위를 주어 선분으로 만들거나 했던 것을 생각하자.
즉, 면의 방정식도 매개변수에 범위를 주어 삼각형으로 만들 수 있다는 것이다.
s+t < 1 의 조건을 만족하면 점 A, B ,C 가 이루는 삼각형이 되고
삼각형 안의 모든 점들을 점 A 와 어떤 벡터와의 합으로 표현된다면
그 벡터는 s = B - A, t = C - A 벡터가 된다. (기저벡터 $\rightarrow$ 아핀조합)

즉 D 가 삼각형 안에 점이 있으면
점 D 를 표현했을 때가 A 와 기저벡터의 덧셈이다.
s+t 의 합이 1보다 작게 나올 것이다.
$$D = A + s \cdot + t \cdot v$$
$$D - A = s \cdot u + t \cdot v$$
$$w = s \cdot u + t \cdot v$$
하지만 s,t 를 구하는 것은 쉽지 않다.
때문에 식에 각각 u 와 v 벡터를 내적한다.
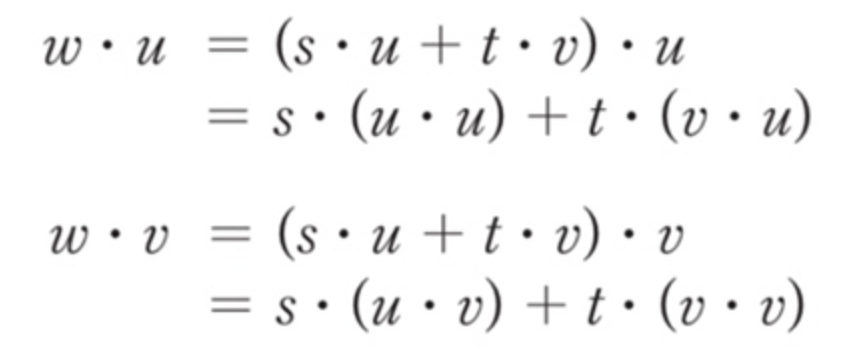
s,t 에 대해서 정리하면 이렇게 나온다.

해당 글의 출처:
https://luv-n-interest.tistory.com/807
아핀 공간, Affine Space - 2 [게임수학]
저번 시간에는 선을 배웠으니 이제 면을 배워볼 시간이다. 선을 만들 때 두 점의 아핀 조합을 통해 만들었다. 면을 만들 때는 세 점의 아핀 조합을 통해서 만든다. 알아보자 면도 매개변수 방정
luv-n-interest.tistory.com
아래 블로그를 이해하며 적었습니다.
'AI > AI 수학' 카테고리의 다른 글
| 초평면 (0) | 2022.11.08 |
|---|---|
| 벡터의 외적 (1) | 2022.11.04 |
| 정규분포 확률밀도함수 유도 (0) | 2022.09.15 |
| ln (x-1) 의 미분 (2) | 2022.08.28 |
| 베이즈 통계학 간단정리 (0) | 2022.01.21 |



