꺼내먹는지식 준
벡터의 외적 본문
벡터의 외적
평행하지 않은 두 벡터가 있다고 가정하자.

두 벡터에게 동시에 수직인 벡터를 구하고 싶으면 어떻게 해야할까?
$\vec{a}, \vec{b}$ 두 벡터가 만드는 평면이 있을텐데, 그 평면 위에서는 두 벡터에 동시에 수직인 벡터를 찾을 수 없다.
이에 따라 벡터의 외적은 기본적으로 3차원 공간에서 생각해야 한다.

$\vec{a}, \vec{b}$ 에 동시에 수직인 벡터 $\vec{P}$ 가 있다고 하자.
해당 $\vec{P}$ 를 쉽게 찾을 수 있는 방법을 찾아보자.
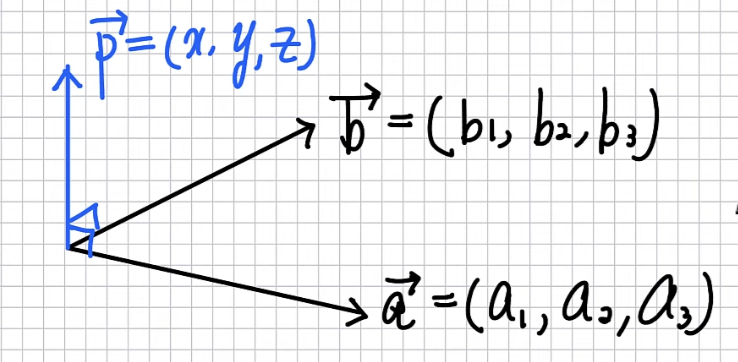
각 벡터를 성분으로 표현하고, 수직인 두 벡터를 내적하면 0이라는 성질을 사용해보자.
$$a_1x + a_2y + a_3z = 0$$
$$b_1x + b_2y + b_3z = 0$$
이 두 식을 동시에 만족시키는 $(x,y,z)$ 를 구하면 $\vec{P}$ 의 성분이다.
$z$ 성분을 없애기 위하여 아래의 작업을 한다.
$$a_1 b_3x + a_2 b_3y + a_3 b_3z = 0 - (1)$$
$$a_3b_1x + a_3b_2y + a_3b_3z = 0 - (2)$$
$(1) - (2) = (a_1b_3 - a_3b_1)x + (a_2b_3 - a_3b_2)y = 0$
만약 $x = a_2b_3 - a_3b_2$ 이고 $y = -(a_1b_3 - a_3b_1)$ 이면 자연스럽게 결과가 성립한다.
이 결과 $z = a_1b_2 - a_2b_1$ 로 얻을 수 있다.
즉, (1), (2) 번식에 모두 성립하는 x,y,z 를 찾을 수 있었고 $\vec{P}$ 는 $\vec{a}$ 와 $\vec{b}$ 모두와 수직임을 알게되었다.
$$ \vec{a} \times \vec{b} = (a_1, a_2, a_3) \times (b_1, b_2, b_3)$$
$$ = (a_2b_3 - a_3b_2, a_1b_3 - a_3b_1, a_1b_2 - a_2b_1)$$
벡터의 외적은 위에서 유도한 것이라고 생각하면 된다.
공식을 암기하지말고 다음과 같이 간단하게 계산하자.




먼저 성분을 모두 작성한 후, $a_1, b_1$ 을 지운다. 그 다음 성분끼리 X 자로 각 곱한 값들을 빼준다. ($a_2b_3 - a_3b_2$)
벡터의 외적은 내적과 달리 결과값도 벡터이다.

다만 벡터의 외적은 다음과 같이 방향이 반대인 경우도 당연히 있을 것이다. 이 때, 외적 결과값 벡터의 방향을 어떻게 알 수 있을까?

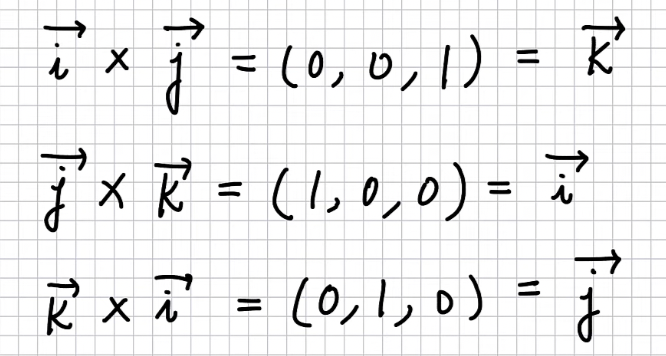

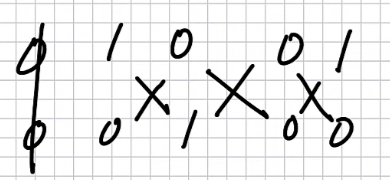
크기가 1 이다 보니 딱 떨어지는 결과가 나왔지만, 두벡터의 외적이 다른 한 벡터의 방향과 동일해진다는 것만을 확인 할 수 있다.
방향을 구할 때는 오른 손의 법칙을 기억하자!

$$ \vec{a} \times \vec{b} = (a_2 b_3 - a_3 b_2, a_1 b_3 - a_3 b_1, a_1 b_2 - a_2 b_1)$$
외적의 크기는 아래와 같다.
$$| \vec{a} \times \vec{b}|^2 = (a_2b_3)^2 + (a_3b_2)^2 - 2a_2a_3b_2b_3 $$
$$ + (a_3b_1)^2 + (a_1b_3)^2 - 2a_1a_3b_1b_3$$
$$ + (a_1b_2)^2 + (a_2b_1)^2 - 2a_1a_2b_1b_2$$
여기에 $(a_1 b_1)^2 + (a_2 b_2)^2 + (a_3 b_3)^2, - (a_1 b_1)^2 - (a_2 b_2)^2 - (a_3 b_3)^2$ 를 더해준다. (합쳐서 0)
그 후 다시 정리를 해주면
※ $\bigg( (\vec{a} \cdot \vec{b})^2 = |\vec{a}|^2|\vec{b}|^2 \cdot \cos^2\theta \bigg)$
$$= (a_1^2+a_2^2+a_3^2)b_3^2 + (a_1^2+a_2^2+a_3^2)b_2^2 + (a_1^2+a_2^2+a_3^2)b_1^2 - (a_1 b_1 + a_2 b_2 + a_3 b_3)^2$$
$$= (a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^3) - (a_1b_1 + a_2b_2 + a_3b_3)^2$$
$$= |\vec{a}|^2 \times |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2$$
$$= |\vec{a}|^2 \times |\vec{b}|^2 \, (1 - cos^2 \theta)$$
$$|\vec{a} \times \vec{b}|^2 = |\vec{a}|^2 \times |\vec{b}|^2 \, (sin^2 \theta)$$
$$(0 \leq \theta \leq \pi) \,\,\, sin \theta \textrm{ 가 양수임을 확인}$$
$$|\vec{a} \times \vec{b}|= |\vec{a}| \times |\vec{b}| \, (sin \theta)$$

벡터의 외적의 성질

1. $(\vec{a} \times \vec{b}) \cdot \vec{a} = 0$ , $(\vec{a} \times \vec{b}) \cdot \vec{b} = 0$

2. $\vec{b} \times \vec{a} = - (\vec{a} \times \vec{b})$
크기는 동일하나 방향이 반대이다.
3. $\vec{a} \times \vec{a} = \vec{0}$
외적의 크기를 구할 때 $\sin \theta(0) = 0$ 이므로
평행한 벡터들도 마찬가지다.

4. $\vec{a} \times \vec{b} = \bigg( |\vec{a}| |\vec{b}| \sin \theta \bigg) \vec{n}$
외적은 평행사변형의 넓이
출처:
해당 글의 내용은 유튜브 수악중독님의 내용을 재편집 한 포스트입니다.
https://www.youtube.com/watch?v=nxiVG22BaZk
https://www.youtube.com/watch?v=PReXlXpEdoM
'AI > AI 수학' 카테고리의 다른 글
| 법선벡터를 이용한 직선의 방정식 (0) | 2022.11.09 |
|---|---|
| 초평면 (0) | 2022.11.08 |
| 아핀 공간 (0) | 2022.11.04 |
| 정규분포 확률밀도함수 유도 (0) | 2022.09.15 |
| ln (x-1) 의 미분 (2) | 2022.08.28 |




