꺼내먹는지식 준
딥러닝 학습모델 간단 정리 본문
비선형 모델 신경망

Fully conneceted layer

화살표: 가중치(W)
선형 모델에 해결하고자 하는 문제에 따라 다른 비선형 활성화 함수가 적용된다.
분류(주어진 데이터가 특정 클래스에 속하는지) 문제를 해결할 경우 softmax 가 필요하다.
softmax
소프트맥수 함수는 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산
$\textrm{softmax}(o) = \textrm{softmax(Wx + b)}$

출력값을 통과시키면 확률벡터를 얻을 수 있다.
특정 클래스에 속할 확률을 파악하고, 분류문제를 풀 수 있다.
추론시에는 최대값만 1로 출력하는 one-hot vector 를 사용한다.
ex)[0.3, 0.1, 0.1, 0.1, 0.1, 0.2] $\Rightarrow$ [1, 0, 0, 0, 0, 0]
활성함수
활성함수는 R 위에 정희된 비선형 함수로 딥러닝에서 중요한 개념
활성함수가 없으면 딥러닝과 선형모형에 차이가 없다.
시그모이드나 tanh 함수는 전통적으로 많이 사용된 활성 함수지만 딥러닝에서 ReLU함수를 많이 쓰고 있다.

https://datascience.stackexchange.com/questions/26475/why-is-relu-used-as-an-activation-function
Why is ReLU used as an activation function?
Activation functions are used to introduce non-linearities in the linear output of the type w * x + b in a neural network. Which I am able to understand intuitively for the activation functions like
datascience.stackexchange.com
오늘날 사용하는 가장 딥러닝의 기본적인 모형이 바로 선형 모델과 활성함수를 반복적으로 사용하는 모형이다.
\[ textrm{H}^{(1)} = \sigma (\textrm{Z}^{(1)}) \]
\[ textrm{Z}^{(1)} = \textrm{X}\textrm{W}^{(1)} + b^{(1)}\]
...
\[ textrm{H}^{(l)} = \sigma (\textrm{Z}^{(l)}) \]
\[ textrm{Z}^{(l)} = \textrm{X}\textrm{W}^{(l)} + b^{(l)}\]

Multi-layer MLP는 신경망이 여러층 합성된 함수이다.
왜 여러층을 쌓을까?
이론적으로는 2층 신경망으로도 임의의 연속함수를 근사할 수 있으나, 실제로 학습을 돌릴 때는 무리가 있다.
층이 깊을수록 목적 함수를 근사하는데 필요한 뉴런의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능하다.

https://deep-learning-study.tistory.com/209
[딥러닝] 신경망의 층을 깊게 하는 것의 중요성
사이토고키의 <밑바닥부터 시작하는 딥러닝>을 공부하고 정리해보았습니다. 층을 깊게 하는 것의 중요성 층을 깊게 하는 것의 중요성은 ILSVRC로 대표되는 대규모 이미지 인식 대회의 결과에서
deep-learning-study.tistory.com
1) 신경망의 매개변수 수가 줄어든다.
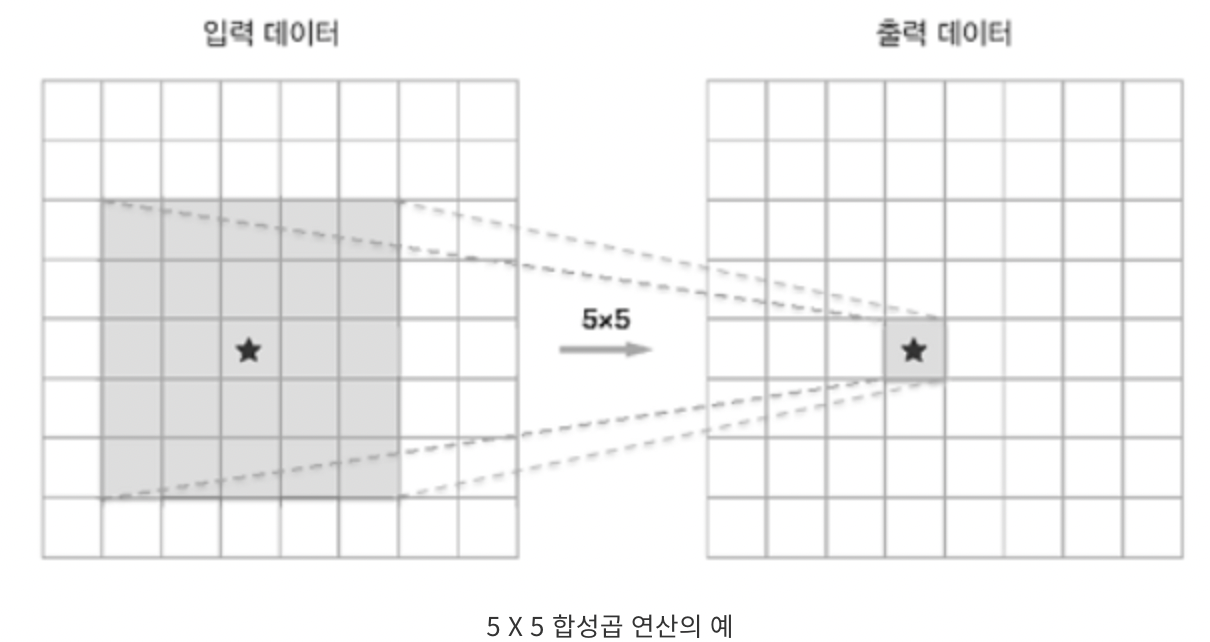
5$\times$ 5 = 25

2 $\times$ 3 $\times$ 3 = 18
2) 학습의 효율성
CNN은 합성곱 계층이 정보를 계층적으로 추출한다. (깊어지면서 텍스처, 사물의 일부와 같이 점차 더 복잡한 것에 반응)
신경망을 깊게하면 학습해야 할 문제를 계층적으로 분해할 수 있다.
3) 정보를 계층적으로 전달
추출한 층의 정보를 다음 층에서 활용하여 더 고도의 패턴을 효과적으로 학습하리라 기대할 수 있다.
그러나 깊은 층으로 복잡한 함수를 근사할 수 있다는 것이 최적화가 더 쉽다는 뜻은 아니다.
복잡하면 할 수록 최적화는 더 많은 노력이 필요하다.
이로인해 Residual Block 의 등장
역전파 알고리즘

각 층에 존재하는 parameter들에 대한 미분을 계산해서 parameter를 업데이트 한다.
행렬들의 모든 개수만큼 경사하강법이 적용되므로 풜씬 더 많은 parameter에 대해서 경사하강법이 적용된다.
딥러닝은 각 층별로 순차적으로 역순으로 계산이 된다.
저층의 gradient vector를 계산할 때 위층의 gradient vector 가 필요하다.
이때 합성함수의 미분법인 연쇄법칙을 사용하여 gradient vector를 전달한다.
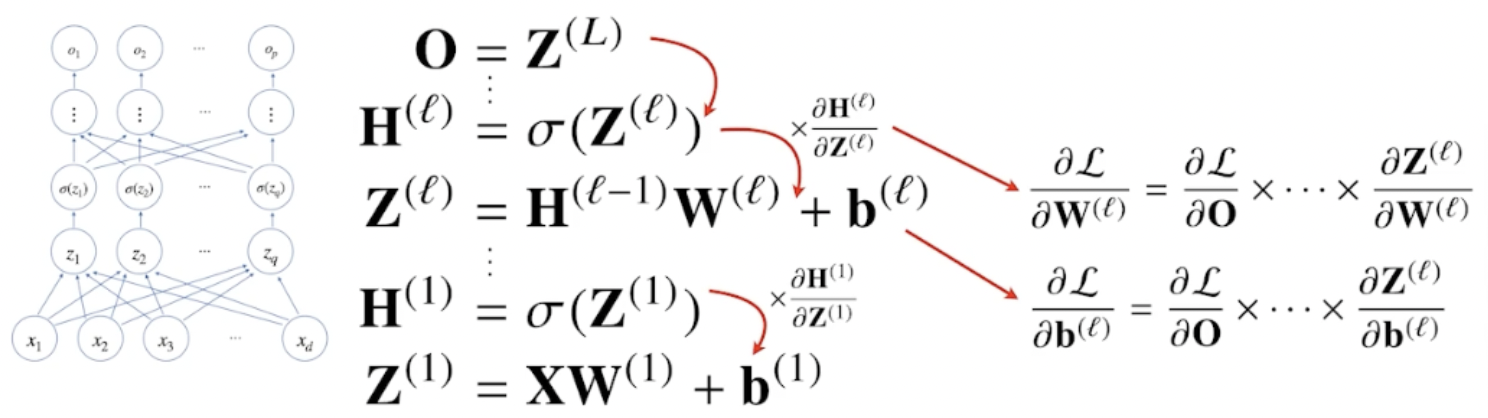
연쇄법칙
\[ z = (x+y)^{2} , \,\,\, \frac{\partial{z}}{\partial{x}} \\ z= w^{2}, \,\,\, w = x+y \]
\[\frac{\partial{z}}{\partial{x}} = \frac{\partial{z}}{\partial{w}} \frac{\partial{w}}{\partial{x}} = 2w \cdot 1 = 2(x+y) \]
예제
\[ \frac{\partial L}{\partial \textrm{W}^{1}} = ?\]

손실함수에 대한 $w^{1}$ 미분을 계산해보면
손실함수를 출력 $o$ 에 대해서 미분을 하고, 그 값을 $h$ 에 대해서 미분을 하고, 그 값을 $z$에 대해서 미분을 하고, 그 값을 $w^{1}$ 에 대해서 미분을 한 것을 순차적으로 곱해지는 형태로 backpropagation이 동작한다.
'AI > 딥러닝 기초' 카테고리의 다른 글
| 딥러닝 역사, 기본 및 용어 (0) | 2022.02.07 |
|---|---|
| Multi_GPU, 분산 학습, 데이터 병렬화, 파라미터서버 (0) | 2022.01.28 |
| 경사하강법 간단정리 (0) | 2022.01.20 |
| 행렬 간단 정리 (0) | 2022.01.19 |
| 벡터 간단 정리 (0) | 2022.01.19 |




