행렬 간단 정리

숫자를 가지는 1차원 배열: 벡터 

벡터를 원소로 가지는 2차원 배열: 행렬 

 

1) 행렬을 이해하는 방법 1 

행렬은 행 벡터를 원소로 가지는 2차원 배열이다. 

 

주로 벡터는 소문자 x, 행렬은 대문자 X 로 표현된다.

n 개의 벡터로 이루어진 행렬 X

n개의 행과 m개의 열 

index는 (행,열) 순 $x_{ij}$

 

 

전치 행렬은 행과 열의 위치를 바꿔준 것, 행렬의 연산에서 많이 사용된다. $x_{ji}$

출처: 부스트 코스 이보다 더 좋은 사진을 못찾아서 사용

벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점을 의미한다. 

즉,행렬을 데이터들의 모임이라 할 때, 행렬의 행벡터 x_{i}는 i 번째 데이터를 의미한다.

각 포인트는 $x_{i}$

ex) i 번째 데이터의 j 번 째 변수 뽑기 

행렬의 성분 곱은 벡터의 성분 곱과 같다. 

행렬의 곱셈은 벡터의 곱셈과 다르다. 

matrix multiplication은 i 번째 행벡터와 j 번째 열벡터 사이의 내적을 성분으로 가지는 행렬이다. (내적: elementwise multiplication 후 덧셈)

사진 출처: https://medium.com/ai%C2%B3-theory-practice-business/fastai-partii-lesson08-notes-fddcdb6526bb

교환 법칙은 성립 되지 않는다. 

X, Y의 전치행렬의 matrix multiplication 

 

 

2) 행렬을 이해하는 방법 2

행렬은 벡터공간에서 사용되는 연산자로 이해될 수 있다. 

출처 부스트 캠프

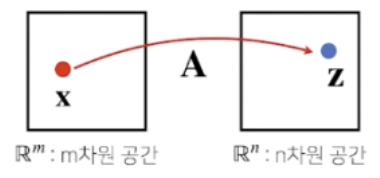
1) 행렬 곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다. 

2) 즉, 서로 다른 차원에 있는 점을 연결 시켜주는 역할을 할 수 있다. 

 

행렬곱을 이용하여 주어진 데이터에서 패턴을 추출할 수도 있고, 주어진 데이터를 압축 할 수도 있다. 

모든 선형 변환은 행렬 곱으로 표현될 수 있다. 

딥러닝은 선형 변환과 비선형의 합성이기 때문에, 행렵 곱의 연산을 먼저 이해하는 것이 필수이다. 

 

 

3) 역행렬

행렬 $A$ 의 연산을 거꾸로 되돌리는 행렬을 역행렬이라 하고, $A^{-1}$ 라 표기한다. 

역행렬은 행과 열의 숫자가 같고, 행렬식(determinant)가 0이 아닌 경우에만 성립한다. 

 

$AA^{-1} = A^{-1}A = I$

 

만약 역행렬을 계산할 수 없다면, 유사 역행렬 혹은 무어 펜로즈 역행렬 $A^{+}$ 을 이용해야 한다. 

 

\[ \left\{ \begin{array}{rl} if \,n \geq m & \mbox{if $A^{+} = (A^{T}A)^{-1}A^{T}$},\\if \,n \leq m & \mbox{if $A^{+} = A^{T}(AA^{T})^{-1}$}\\ \end{array} \right. \]

각 경우만 성립한다. 

$n \geq m: A^{+}A = I$

$n \leq m: AA^{+} = I$

 

유사 역행렬은 행과 열의 숫자가 달라도 계산해볼 수 있다. 이때 기호는 -가 아니라 + 를 사용한다. 

행이 더 많을 때, 열이 더 많을 때 계산하는 방법이 다르다. 

n과 m 의 개수가 같지 않을 때,

$Ax = b$

$x = A^{+}b = A^{T}(AA^{T})^{-1}b $

1) 변수의 개수가 식의 개수보다 많은 경우: 연립 방정식을 풀 수 있다. 
2) 변수의 개수보다 식의 개수가 많은 경우(변수보다 데이터가 더 많은 경우): 선형 회귀에서 많이 보는 상황.유사 역행렬을 사용해서 데이터를 표현하는 선형 모델을 해석했을 때 선형 모델에 해당하는 선형 회귀식을 찾을 수 있다. 

 

$X\beta = \hat{y} \sim y$

$\beta = X^{+}y = (X^{T}X)^{-1}X^{T}y$