꺼내먹는지식 준
통계학 간단정리 본문
모수
통계적 모델링은 적절한 가정 위에서 확률 분포를 추정하는 것이 목표, 기계 학습과 통계학이 모두 공통적으로 추구하는 목표
그러나 유한한 데이터로 모집단 분포를 정확하게 알아낼 수 없기에 근사적으로 확률 분포를 추정한다. (불확실성을 고려하여 위험을 최소화)
데이터가 특정 확률 분포를 따른다고 선언한 후, 그 "분포를 결정하는 모수"를 추정하는 방법을 parameteric 방법론이라 한다.
특정 확률 분포를 가정하지 않고, 데이터에 따라 모델의 구조 및 모수의 개수가 유연히 바뀌면 nonparameteric 방법론(모수가 없는게 아님)이라 부른다.
ex) 정규분포라 가정하면 평균, 분산이 모수이다. 이 두가지를 추정하는 방법을 통해 데이터를 학습하는 방법을 paramtetric 방법론의 예시. 대부분의 기계학습은 nonparameteric 방법론
확률 분포 가정
히스토 그램 모양 관찰
1) 데이터 2개의 값만(0 또는 1) 가지는 경우 : 베르누이 분포
2) 데이터가 n개의 이산적인 값을 가지는 경우 : 카테고리 분포
3) 데이터가 [0,1] 사이에서 값을 가지는 경우 : 베타 분포
4) 데이터가 0 이상의 값을 가지는 경우 : 감마 분포, 로그 정규 분포 등
5) 데이터가 R 전체에서 값을 가지는 경우 : 정규분포, 라플라스 분포 등
기계적으로 확률 분포를 가정하면 안 되고, 데이터 생성 원리를 고려하고 데이터를 먼저 관측을 해야 한다.
데이터로 모수 추정
데이터의 확률 분포 가정 후, 모수를 추정해볼 수 있다.
표본 평균
\[ \bar{X} = \frac{1}{N}\sum_{i=1}^{N}X_{i} \]
\[ E[\bar{X}] = \mu \]
표본분산
\[ S^{2} = \frac{1}{N-1}\sum^{N}_{n-1}(X_{i} - \bar{X})^2 \]
\[ E[S^{2}] = \sigma^{2} \]
통계량의 확률분포(표본들의 분포가 아니라 표본 평균과 표본 분산의 확률 분포)를 표집 분포 Sampling distribution (!= sample distribution 표본 분포)이라 한다.
중심극한 정리
표본 평균의 표집 분포는 N이 커질 수록 정규분포를 따른다.
모집단이 정규분포를 따르지 않아도 동일하다. (표본 평균의 분포니까)
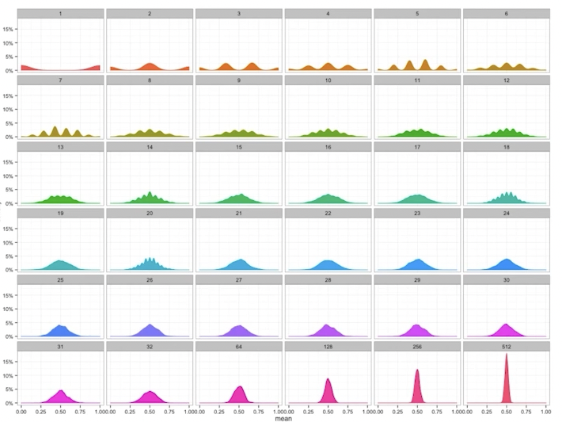
표본 평균의 분산은 N 이 늘어나면 분산이 점점 0에 가까워 진다. 하나의 값으로 몰린다.
최대가능도 추정법
표본평균이나 표본분산은 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라진다.
이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(MLE) 이다.
\[ \hat{\theta}_{MLE} = \underset{\theta}{\textrm{argmax}} \,L(\theta ; x) = \underset{\theta}{\textrm{argmax}} \, P(x|\theta) \]

가능도 함수는 모수 $\theta$를 따르는 분포가 x를 관찰할 가능성을 뜻하지만 확률로 해석하면 안된다.
원래 확률 밀도 함수는 $\theta$ 즉 모수가 주어졌을 때 x에 대한 함수로 해석을 하나,
가능도 함수는 주어진 데이터 x에 대하여 모수 $\theta$를 변수로 둔 함수 : 데이터가 주어진 상황에서 $\theta$를 변형시킴에 따라 값이 바뀌는 함수
가능도 함수는 모수 $\theta$ 를 따르는 분포가 데이터 x를 관찰할 가능성을 뜻한다. (확률이 아니다. $\theta$를 적분한다고 1이 되지 않는다.)
주어진 X에 대해 $\theta$에 따른 가능성의 분포를 통해, 최대 가능성을 관측할 수 있다.
데이터 집합 X가 독립적으로 추출되었을 경우, 로그가능도를 최적화 한다.
\[ L(\theta, X) = \prod^{n}_{i=1}P(x_{i}|\theta)\, \Rightarrow \log\,L(\theta, X) = \sum^{n}_{i=1}\log P(x_{i}|\theta) \]
로그 가능도를 사용하는 이유
1) 로그 가능도를 최적화하는 모수 $\theta$ 는 가능도를 최적화하는 MLE 가 된다.
2) 데이터의 숫자가 많은 경우 컴퓨터의 정확도로 가능도를 계산하는 것을 불가능해진다. (0보다 작은 값이 무수한 곱셈은 오차가 크게 발생)
3) 데이터가 독립인 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꾸어 컴퓨터 연산을 가능하게 할 수 있다.
4) 경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하는데, 로그 가능도를 사용하면 연산량을 $O(n^{2})에서 O(n)$ 으로 줄여준다.
5) 대게 손실함수의 경우 경사하강법을 사용하므로, 음의(최소화하기위해) 로그가능도를 최적화한다.
ex) 정규분포를 따르는 확률변수 X 로부터 독립적인 표본 $[x_{1}, ..., x_{n}]$을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
\[ \log \, L(\theta ; X) = \sum^{n}_{i=1} \log P(x_{i}|\theta) = \sum^{n}_{i=1} \log \frac{1}{\sqrt{2\pi\sigma^{2}}} e^{-\frac{|x_{i}-\mu|^{2}}{2\sigma^{2}}}\]
\[ = -\frac{n}{2}\log2\pi\sigma^{2} - \sum^{n}_{i=1} \frac{|x_{i} - \mu|^{2}}{2\sigma^{2}} \]
왼쪽 수식은 분산, 오른쪽 수식은 평균과 분산
모수 평균과 sigma에 대해서 오른 쪽 수식을 미분해서 최적화 해볼 수 있다.
\[ \frac{\partial \log L} {\partial \mu} = - \sum^{n}_{i=1}\frac{x_{i}-\mu}{\sigma^{2}} \]
\[ \frac{\partial \log L} {\partial \sigma} = -\frac{n}{\sigma} + \frac{1}{\sigma^{3}} \sum^{n}_{i=1}|x_{i}-\mu|^{2} \]
미분을 해서 최대 가능도를 구하고 싶으면, 미분 했을 때 각각의 parameter에 대해서 0이 되는 점을 찾아주면 된다.
순간 변화율이 0이되는 $\mu , \sigma$를 구하면 log likelihood 를 최대화 해주는 parameter 이다.
\[ \hat{\mu}\textrm{MLE} = \frac{1}{n}\sum^{n}_{i=1}x_{1} \]
\[\hat{\sigma}^{2}\textrm{MLE} = \frac{1}{n}\sum^{n}_{i=1}(x_{i} - \mu)^{2}\]
https://angeloyeo.github.io/2020/07/17/MLE.html
최대우도법(MLE) - 공돌이의 수학정리노트
angeloyeo.github.io
다음 블로그에 완벽한 유도 과정이 담겨있다.
카테고리 분포에서의 최대가능도 추정법 예제는 그냥 듣고 넘어가자.
https://namyoungkim.github.io/statistics/2017/09/17/probability/
2017-09-17-probability
N개의 독립 샘플이 있는 경우, Likelihood $$ \begin{eqnarray*} L(\theta ; x_{1:N}) &=& P(x_{1:N};\theta) \\ &=& \prod_{k=1}^N P(x_i;\theta_i) \\ &=& \prod_{i=1}^N \prod_{k=1}^K \theta_k^{x_{i,k}} \end{eqnarray*} $$ Log-Likelihood $$ \begin{eqnarra
namyoungkim.github.io
*라그랑주 승수법
딥러닝에서 최대가능도 추정법
최대가능도 추정법을 이용해서 기계학습 모델을 학습할 수 있다.
딥러닝 모델의 가중치를 $\theta = (W^{1} ... W^{L})$ 라 표기했을 때, 분류 모델에서 소프트맥스 벡터는 카테고리분포의 모수 (p_{1}, ... p_{k}) 를 모델링 한다.
원핫벡터로 표현한 정답레이블 y = (y_{1}, ..., y_{k}) 을 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화할 수 있다d.
\[ \hat{\theta}_{\textrm{MLE}} = \underset{\theta}{\textrm{argmax}} \frac{1}{n} \sum^{n}_{i=1}\sum^{K}_{k=1}y_{i,k}\log(\textrm{MLP}_{\theta}(x_{i})_{k}) \]
k = 1 ~ k 모든 클래스의 개수에 대해, i =1 ~ n 모든 데이터에 대해,
multi perceptron의 k번째 예측값의 log 값과 정답 label에 해당하는 y의 k번째 주소값을 곱해준 것들에 덥셈들로 표현을 했다.
기계 학습에서 사용되는 손실함수들은 기계 학습 모델이 학습하는 확률 분포와 데이터에서 관측되는 확률 분포의 거리를 통해 유도할 수 있다.
데이터 공간에 두 개의 확률 분포 $P(x), Q(x)$ 가 있을 경우 두 확률분포 사이의 거리는 다음의 방법으로 계산한다.
1) Total Variation Distance, TV
2) Kullback-Leibler Divergence, KL
3) Wasserstein Distnace
Kullback-Leibler Divergence, KL
KL 을 이해하기 위해서 Information Entropy에 대한 선행 이해는 필수이다.
https://angeloyeo.github.io/2020/10/26/information_entropy.html
정보 엔트로피(information entropy) - 공돌이의 수학정리노트
angeloyeo.github.io
항상 신세지고 있는 공돌이 님이다.
http://tensorboy.com/cross-entropy
Cross Entropy
cross entropy loss
tensorboy.com
관점에 따라 '정보'를 다르게 해석할 수 있다.
데이터 베이스의 정보는 데이터를 쉽게 사용할 수 있도록 가공한 것이다.
통계학에서 수학적으로 정보란 무엇일까?
바로 깜짝 놀랄만한 정도(degree) 줄여서 깜놀도라고 기억을 하자.
즉, 내용이 놀랄만할 수록 정보량이 많다는 뜻이다.
이 개념은 확률 개념의 재해석이라 볼 수 있다.
확률이 낮은 사건일 수록 거의 일어나지 않을 일이기에 정보량이 높다.
즉, 수식으로 정의하면 확률 값과 정보량은 반비례 할 것이다.
랜덤 변수 X에 대해 정보량은 다음과 같이 표현할 수 있다.
\[ 정보량 \propto \frac{1}{P(X)} \]
통계학에서 정보량은 다음과 같이 정의 된다.
\[ I(x) = - \log_{b}(P(x))\]
로그의 밑 b는 응용분야에 따라 2,e,10 (bit, nit, dit)등 다르게 쓰인다.
일단 정보량에 정의에 음수가 붙은건, 정보량 정의에 log가 사용되서이다.
\[ \log_{b}(\frac{1}{P(x)}) = - \log_{b}(P(x)) \]
정보량에 log가 붙은 이유는 다음과 같다.
1) 확률값에 반비례 해야 한다.
2) 두 사건의 정보량을 합치면 각 사건의 정보량을 합친 것과 같아야 한다.
엔트로피
통계학에서 (정보) entropy는 평균 정보량을 뜻한다.
열역학에서의 entropy와 연결하지말자.
통계학의 entropy는 열역학의 Gibb's entropy의 수식과 유사점이 있고, 연결점을 찾을 수는 있다. 하지만 새로운 관점에서 정보 엔트로피를 배운다고 생각해보자.
이산 랜덤변수 X의 샘플 공간이 ${x_{1},x_{2},...,x_{n}}$ 일 때, 정보 엔트로피는 다음과 같다.
\[ H(X) = E[I(X)] = -\sum^{n}_{i=1}P(x_{i})\log_{b}(P(x_{i})) \]
다음의 예시를 보자.
주사위 1부터 6까지의 눈이 나오면 각각 100원부터 600까지 수령한다.
이때의 기댓값은 다음과 같다.
\[ 기댓값 = \frac{1}{6}\times 100 + \frac{1}{6}\times 200 +... + \frac{1}{6}\times 600\\ = \sum^{6}_{i=1}P(x_{i})M(x_{i})\]
\[ M(_{x_{i}}) \textrm{는} x_{i} \textrm{라는 사건 발생에 대해 받는 돈 100 ~600원} \]
즉, 기댓값의 정의는 일어날 수 있는 확률 $\times$ 이벤트 값을 모두 합친 것이다.
다시말해, $-\log_{b}(P(X_{i}))$ 는 이벤트 값이다.
정리하자면, 정보 엔트로피는 모든 일어날 수 있는 확률 $\times$ 정보량(이벤트) 값을 합친 것이므로, 계산식이 다음과 같다.
\[ H(X) = E[I(X)] = -\sum^{n}_{i=1}P(x_{i})\log_{b}(P(x_{i})) \]
Binary case의 크로스 엔트로피
Binary case에는 출력이 0 혹은 1 두가지 경우이다. ex) 남자, 여자
binary case의 cross entropy 는 다음과 같다.
$y$가 타겟값, $\hat{y}$가 예측값이라 할 때,
\[ BCE = -y\log(\hat{y}) - (1-y)\log(1-\hat{y}) \]
1) $y = 1, \hat{y} = 1 인 경우 , y=0, \hat{y} = 0으로 타겟 값을 맞춘경우 $
\[ BCE = -y\log(\hat{y}) - (1-y)\log(1-\hat{y})\\ = -(1)\cdot\log(1) - (0)\cdot\log(0) = 0\\ = -(0)\cdot\log(0) - (1)\cdot\log(1) =0 \]
BCE(Binary Cross Entropy) 값은 0 이 된다.
2)1) $y = 1, \hat{y} = 0 인 경우 , y=0, \hat{y} = 1으로 타겟 값을 못 맞춘 경우 $
\[ BCE = -y\log(\hat{y}) - (1-y)\log(1-\hat{y})\\ = -(1)\cdot\log(0) - (0)\cdot\log(1) = \infty \\ = -(0)\cdot\log(1) - (1)\cdot\log(0) =\infty \]
BCE 값은 $\infty$ 가 된다.
여러가지 출력 case를 가지는 경우의 Cross Entropy
지금까지 과정에서 Cross Entropy 값이 타겟값과 모델 출력값이 얼마나 다른지에 대해 표현한 것임을 알 수 있다.
즉 CE 의 식을 참고하여, 이렇게 쓸 수 있다.
\[ BCE = \sum_{x \in 0,1}(-P(x)\log(Q(x))) \]
여기서 $P(x)$는 희망하는 타겟에 대한 label 값이고, Q(x)는 모델에서 출력한 출력 값이다.
이를 좀 더 일반화 하면, 여러가지 출력을 갖는 경우에 대한 cross entropy를 정의할 수 있다.
\[ CE = \sum_{x \in X}(-P(x)\log(Q(x))) \]
CE는 Q라는 모델의 결과에 대해 P 라는 이상적인 값을 기대했을 때 우리가 얻게되는 놀라움에 대한 값을 정보량으로 표현한 것이다.
특이한 주사위가 하나 있다고 하자,

Cross Entropy를 계산하면,
\[ \Rightarrow \, -\sum_{i}P(x_{i})\log(Q(x_{i})) = - \Bigg(\frac{1}{6}\log_{2}\bigg(\frac{1}{2}\bigg) + \frac{5}{6}\log_{2}\bigg(\frac{1}{10}\bigg) \Bigg) = 2.9349 bit\]
여기선 주사위 값의 차이는 의미가 없다고 본 듯 하다. 돈이었다면, 그 $\frac{1}{6}$ 자리에 금액이 들어갔을 것
일반적인 주사위
\[ \Rightarrow \, -\sum_{i}P(x_{i})\log(Q(x_{i})) = - \Bigg(\frac{6}{6}\log_{2}\bigg(\frac{1}{6}\bigg) = 2.5850 bit\]
Kullback-Leibler Divergence, KL
KL divergence는 "divergence"에 주목하면 된다. 이 단어는 "발산"이라는 의미를 갖는 것이 아니라, "차이"라는 의미이다.
여기서 "차이"는 두 확률 분포의 비교를 뜻한다. 이상적인 분포를 근사하는 다른 분포를 샘플링할 때 발생하는 정보 엔트로피 차이를 계산할 때 사용.
Relative entropy, informaion gain 이라고도 함.
우리의 목적이 확률 분포 P 를 정확히 모델링 하는 것 일 때,
이산확률분포 P와 Q가 동일한 샘플 공간 X에서 정의된다고 하면 KL divergence는 다음과 같다.
\[ D_{KL}(P||Q) = \sum_{x\in X}P(x)\log_{b}\bigg( \frac{P(x)}{Q(x)} \bigg) \]
*|| 는 거리(차이)를 뜻함
로그의 밑 b는 2,10, e 중에 사용되며, 이 때 각각의 정보량 단위는 bit, dit, nit 이다.
\[ = \Rightarrow -\sum_{x \in X}P(x)\log_{b}\bigg( \frac{Q(x)}{P(x)} \bigg) \]
\[ = \Rightarrow -\sum_{x \in X}P(x)\log_{b} Q(x) + \Rightarrow -\sum_{x \in X}P(x)\log_{b} P(x) \]
각 항은 기댓값으로 치환해볼 수 있다.
\[ \Rightarrow -E_{P}[\log_{b}Q(x)] + E_{p}[log_{b}P(x)] \]
* 여기서 기댓값 연산자 E에 붙은 subscript 'P'는 P(x)라는 확률분포에 대한 기댓값 연산임을 의미
\[ \Rightarrow H_{P}(Q) - H(P)\]
$H_{P}(Q)는 P의 기준으로 봤을 때의 Q에 대한 크로스 엔트로피이고 H(P)는 P에 대한 정보 엔트로피이다.$

https://engineer-mole.tistory.com/91
[수학/분포] 정규분포 간의 KL 발산(쿨백-라이블러 발산 ; Kullback–Leibler divergence, KLD)
위키피디아에 있는 쿨백-라이블러 발산(Kullback–Leibler divergence, 이하 KLD)의 정의에 대해 잠깐 정리하자면, 다음과 같다. KLD는 두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상
engineer-mole.tistory.com
http://tensorboy.com/kullback-leibler-divergence
KL divergence
Kullback–Leibler divergence
tensorboy.com
분류 문제에서 정답레이블을 P, 모델 예측을 Q라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화 하는 것과 같다.
'AI > AI 수학' 카테고리의 다른 글
| 아핀 공간 (0) | 2022.11.04 |
|---|---|
| 정규분포 확률밀도함수 유도 (0) | 2022.09.15 |
| ln (x-1) 의 미분 (2) | 2022.08.28 |
| 베이즈 통계학 간단정리 (0) | 2022.01.21 |
| 확률론 찍먹 (MCMC) (0) | 2022.01.20 |



