꺼내먹는지식 준
고윳값, 고유벡터 (eigen value, eigen vector) 본문
https://www.youtube.com/watch?v=7dmV3p3Iy90
해당 내용은 공돌이의 수학정리노트를 정리한 내용
이 블로그는 내가 보고 기억하려고 적는것이고, 이 글보다는 위 영상을 보는 것이 이해에 훨씬 도움이 된다.

https://angeloyeo.github.io/2019/07/17/eigen_vector.html
해당 사이트에서 vector에 곱해지는 matrix 값들을 변경시켜보며 감을 익혀볼 수 있다.

※ diagonal 값은 벡터의 길이를 조정한다. 이로인해 만약 diagonal 값 외에 모든 값이 0일 때 diagonal 값이 0 이 되면 차원이 축소된다.
※ 이 시연을 통해 벡터에 행렬 연산을 취하면 원래 벡터와 다른 벡터 결과 값을 얻는 다는 것을 확인했다.
그러나 어떤 벡터들은 선형 변환 시 크기만 바뀌고 방향이 바뀌지 않을 수 있다.
예시)


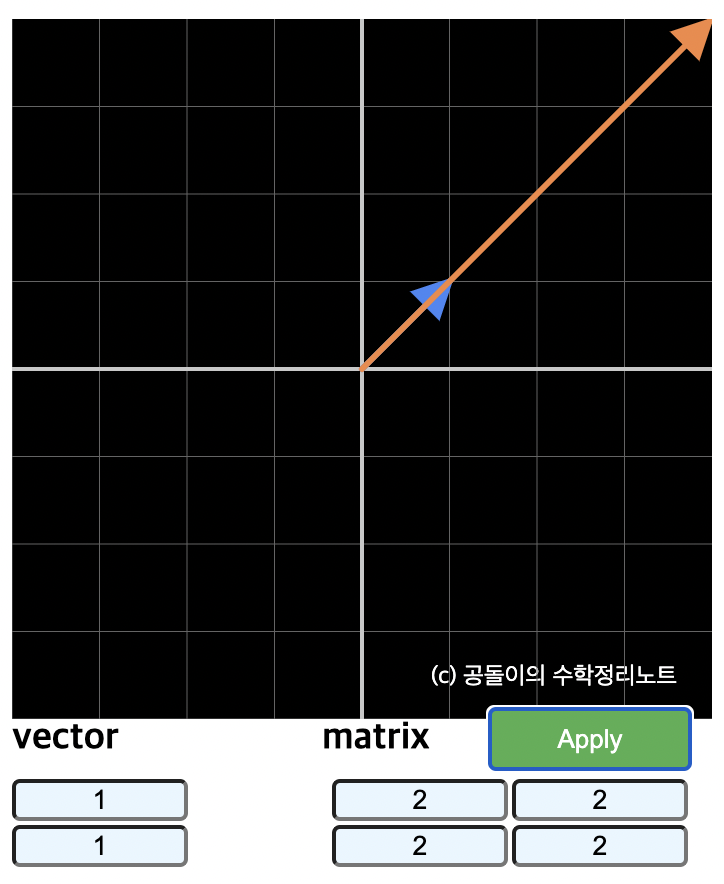

즉, 고윳값과 고유벡터가 물어보는 것은 아래와 같다.
- 벡터 $\vec{x}$ 에 선형변환 $A$ 를 취했을 때, 그 크기만 변하고 원래 벡터와 평행한 벡터 $\vec{x}$ 는 무엇인가요?
- 그렇다면, 그 크기는 얼마나 변했나요?
이때 고유벡터는 $x (\vec{x})$ , 고유값은 $\lambda$ 가 된다.
정리하자면, 고윳값과 고유벡터의 정의는 아래와 같다.

이로인해, 고유값과 고유벡터를 계산하기 위해서는 다음 과정을 거친다.
$$A\vec{x} = \lambda\vec{x}$$
$$\rightarrow A\vec{x} = \lambda I \vec{x}$$
$$\rightarrow (A-\lambda I)\vec{x} = \vec{0}$$
여기서 $\vec{x} != 0$ 인 경우를 만족하기 위해서는 $A-\lambda I$가 역행렬을 가져서는 안된다.
즉, $det(A-\lambda I) = 0$ 이어야 한다.

예시문제
아래와 같은 행렬 $A$에 대한 고윳값과 고유벡터를 계산하시오.
$$A = \left[ \begin{matrix} 2 & 1 \\ 1 & 2 \\ \end{matrix} \right]$$
$$A\vec{x} = \lambda\vec{x} $$
$$ (A-\lambda l) \vec{x} = \vec{0} $$
$$ det(A-\lambda l) = 0$$
$$ det( \left[ \begin{matrix} 2-\lambda & 1 \\ 1 & 2 - \lambda \\ \end{matrix} \right]) = 0$$
$$ (2-\lambda)^2 - 1 = 0$$
$$ \lambda^2 - 4\lambda + 4 - 1 = 0$$
$$ \lambda^2 - 4\lambda + 3 = 0$$
$$\Rightarrow \lambda_1 = 1, \lambda_2 = 3$$
$ \lambda_1 = 1 \textbf{인 경우} $
$2x_1 x_2 = x_1 $
$x_1 + 2x_2 = x_2$
$\Rightarrow -x_2 = x_1$
대충 비율만 맞추면 되므로, $x_1 = 1, x_2 = -1$
고유벡터는 아래와 같이 1로 맞춰주거나
$$ \left[ \begin{matrix} x_1 \\ x_2 \end{matrix} \right] = \left[ \begin{matrix} 1 \\ -1 \end{matrix} \right] $$
혹은 벡터의 크기를 참고하여
$$ \left[ \begin{matrix} x_1 \\ x_2 \end{matrix} \right] = \left[ \begin{matrix} \sqrt{2} \\ -\sqrt{2} \end{matrix} \right] \cdot t \,\, (t \in \mathbb{R})$$
라고 표현하기도 한다.
$\lambda_2 = 3 \textbf{인 경우}$
$v_2 = \left[ \begin{matrix} 1 \\ 1 \end{matrix} \right]$


예시)

'AI > 추천시스템' 카테고리의 다른 글
| Item2Vec (0) | 2022.07.19 |
|---|---|
| Collaborative Filtering - 2 (Model based CF, Matrix Factorization, Bayesian Personalized Ranking) (0) | 2022.07.15 |
| Collaborative Filetering - 1 (Neighborhood-based CF, K- Nearest Neightborhood CF) (0) | 2022.07.11 |
| TF-IDF 추천 (0) | 2022.07.07 |
| 추천 시스템 공부 로드맵 (0) | 2022.07.05 |




