꺼내먹는지식 준
머신러닝 정리 4.5(4) - Gradient Boost 본문
Gradient Boost는 굉장히 다양한 분야에 적용 가능하도록 디자인 된 알고리즘이다. 하지만 주로 continous value를 예측하는 모델로 사용되고, 나머지도 분류 모델 정도로 사용된다.
본 글에서는 먼저 회귀 모델로의 Gradient Boost를 다루고 분류 모델로의 Gradient Boost를 다뤄본다.
회귀 모델로의 Gradient Boost
AdaBoost 와 Gradient Boost의 차이
AdaBoost를 잘 모르면 이 글을 읽고오자.

위와 같은 데이터 샘플들이 주어졌다고 가정해보자.


AdaBoost 는 여러개의 stump의 결합으로 의사결정을 하는 머신러닝 기법이다. 선행 stump가 잘 분류하지 못했던 샘플들에 대하여 후행 stump가 얼마나 잘 분류했는가에 따라 각자 다른 Amount of Say 가 주어지고, 새로운 input이 들어오면 내린 결정 * Amount of Say로 최종 output 을 결정한다. (투표권에 차등이 있다고 생각하면 편하다) 당연히 stump를 결정할 때도 선행 stump가 잘 분류하지 못했던 샘플을 기반한다. 사용자가 요청한 stump의 개수 혹은 완벽하게 샘플을 모두 분류해낼 때 까지 위 과정을 반복한다.
Gradient Boost는 선행 트리의 오류를 후행 트리가 반영한다는 점에서 AdaBoost와 유사하나, 주로 tree의 사이즈가 stump 보다 크다. 본 글에서는 주로 leaf 의 개수를 4개로 제한해서 설명할 예정이나, 현업에서는 주로 8~ 32개 정도로 제한한다. 즉, AdaBoost나 Graident Boost 모두 선행 트리의 오류를 반영하여 고정된 사이즈의 트리를 만든다는 점에서는 동일하나 Gradient Boost의 각 트리가 stump 보다 클 수 있다는 점이 다르다. 또한 AdaBoost와 Gradient Boost 모두 최종 output에 대한 각 트리 별 결정 발언권을 조정하나, Gradient Boost의 모든 트리는 결정권의 크기를 동일하게 본다. (즉 Gradient Boost는 모든 tree의 결정권 크기를 동시에 조정 가능)
Gradient Boost 작동 원리

Gradient Boost의 작동 원리는 반복 과정을 통해 label 예측을 개선시켜 정답에 가깝게 하는 것이다.
Initial 예측은 주어진 정보가 따로 없으므로, label (Weight)의 평균을 사용한다.

즉, Weight의 평균은 우리가 첫번째로 예측한 값이다.
예측값을 기존 관측값인 Weight 샘플 값들에서 각각 뺀다. (예측 값 - 관측 값)은 Residual이라 부른다.

Residual 값을 분류하는 Tree를 만든다. 목표는 label과 예측값의 차이인 Residual 값을 점점 작게 만드는 것이다. 내용을 끝까지 따라오면 충분히 이해할 수 있다.

다음과 같은 Tree를 통해 Residual 값을 분류한다. 해당 Tree를 만드는 방법은 Regression Tree와 동일 할 것으로 추측된다. 현재 Tree의 leaf 는 4개이나, 현업에서는 보통 8~ 32개를 사용한다는 점을 기억하자.
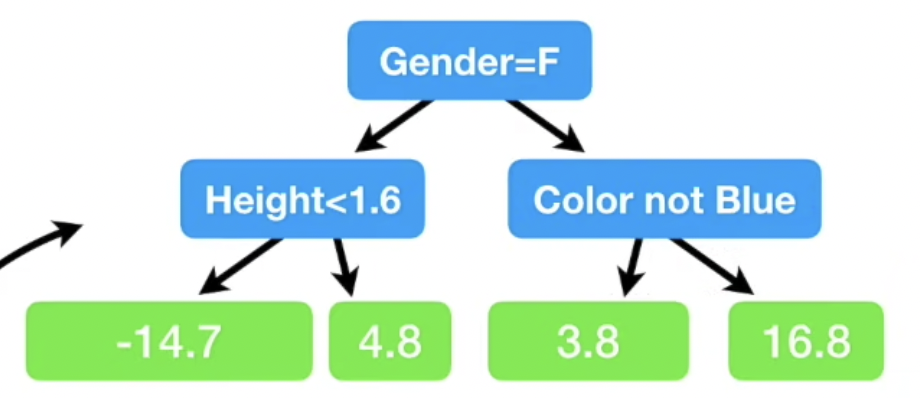
각 leaf 에 해당하는 값이 여러개인 경우 평균을 취한다. 왜 평균 취하는 이유는 아래 공식을 통해 유도되는 과정을 참고하자.
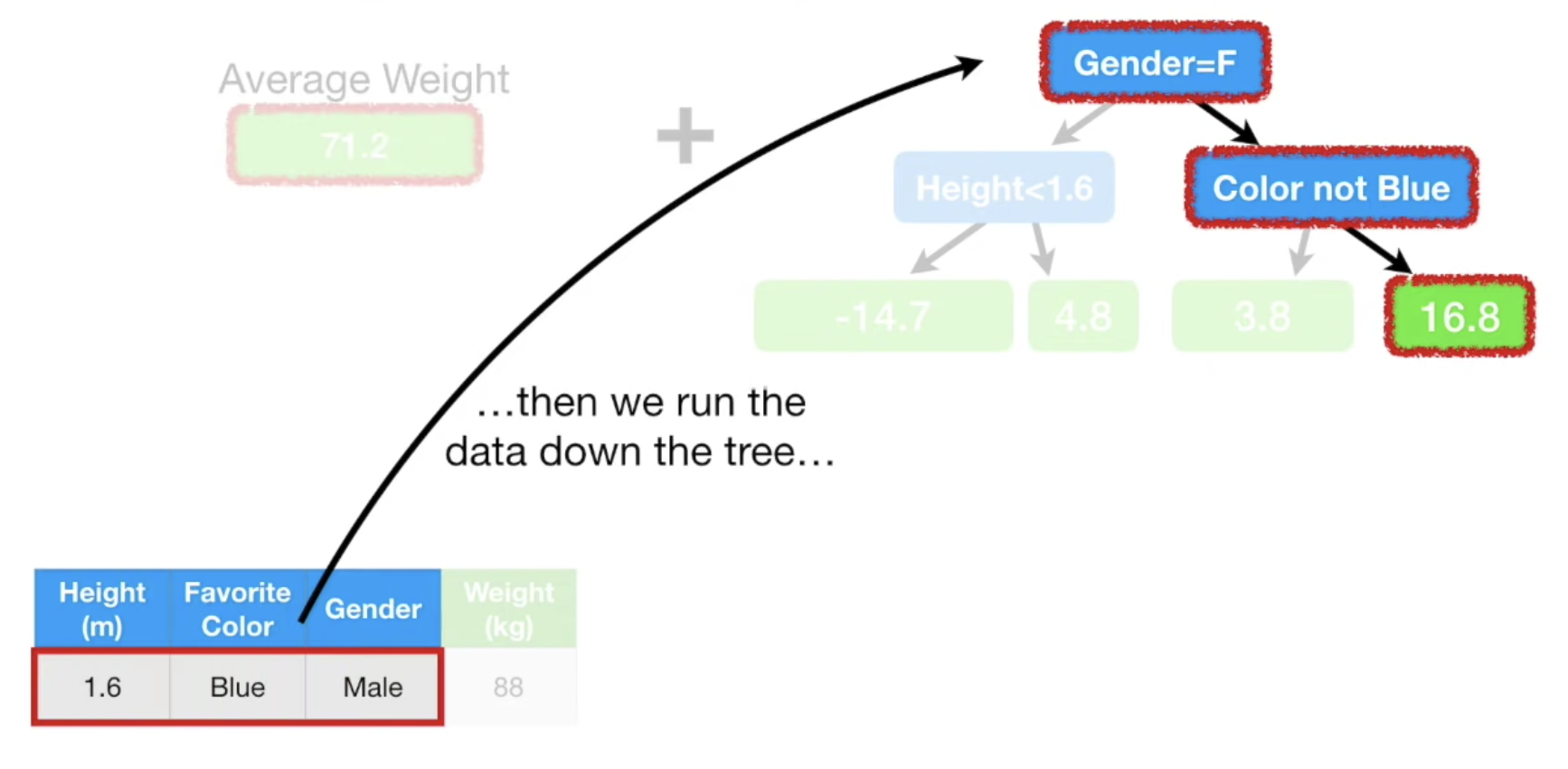

트리를 통해 분류한 residual 값과 Initial 예측값을 이용하여 분류 기준에 해당되었던 데이터 샘플의 weight 값을 update한다.
한번의 과정만 거쳤는데 실제 Weight값을 복원했다. 무슨 뜻일까? 안봐도 데이터에 Over-fitting 되었다는 증거다.
여기서 Learning Rate 개념이 도입된다.


Learning Rate란 한번에 큰 값을 업데이트 하지 말고, 조금씩 목표 지점에 도달하자는 개념인건 딥러닝을 하시는 분들은 바로 이해할 수 있을 것이다. 정리하자면 0~ 1 사이 값을 갖는 Learning Rate * residual 로 예측값을 업데이트 한다. 새로운 예측값 72.9 라는 값이 한번에 88까지 접근 했던 초기 방식에 비해 훨씬 더 천천히 접근하지만, initial 예측값이던 71.2 보다는 더 좋은 결과임에는 틀림없다. Graident Boost를 제안한 Jerome Friedman의 emprical 실험 결과에 따르면, Learning Rate를 통해 옳은 방향으로 조금씩 나아가는 방식이 더 낮은 Variance 즉, 타당한 예측값을 만들어낸다.


새로운 예측 값을 통해 Residual 을 업데이트해보니, 확실히 이전 Residual 보다 결과가 더 낫다.
위 과정을 반복한다. 반복 과정 중, Residual을 분류하는 Tree는 당연히 새롭게 만들어 지기도 한다. (여기서는 편의를 위해 동일한 Tree를 사용하였다.)

반복 과정에서 초기 예측 값, 이후 반복 과정에서 구한 각각의 residual X Learning Rate을 더해 예측값을 업데이트한다.

반복 과정에서 Residual 은 계속해서 작아진다.
우리가 정한 최대 반복 횟수, 혹은 resiual 값이 더이상 변화가 없을 때 학습을 멈춘다.

이후 모델에 예측을 위해 Input 데이터가 들어오게 되면,

학습과정에서 생성하였던 initial Value + 각 트리의 Residual * learning rate 를 통해 최종 예측 값을 산출한다.
Gradient Boost 이론 (Regression)

Data 샘플 $x_i, y_i$ 가 총 n 개 존재하고, Loss function은 미분 가능해야 한다.
Regression을 수행하는 Gradient Boost가 주로 사용하는 Loss function은 아래와 같다.
$\frac{1}{2} \textrm{ (Observed - Predicted)}^2$
앞에 $\frac{1}{2}$ 가 붙어있는 이유는 Gradient Boost의 Loss function을 미분하면 합성함수으로 인해
$-\textrm{Observed - Predicted}$ 가 된다. 미분 결과가 -Residual 이이 되는 것을 알 수 있다.
$L(y_i, F(x))$ 에서 $y_i$ 가 Obeserved 이고, $F(x)$ 가 predicted 이다.
(물론 Loss function은 다른 것도 있다.)

$y_i$ 는 observed, $\gamma$ 는 predicted 이다.
아래와 같은 데이터 샘플이 주어졌을 때,

i = [1 , n] 을 모두 더하면 아래와 같이 된다.

$argmin_\gamma$는 총 합을 최소화 하는 predicted 의 값이라는 뜻이다.
오른쪽 그래프와 같이, predicted 값에 따른 $F_0(x)$를 알 수 있다.
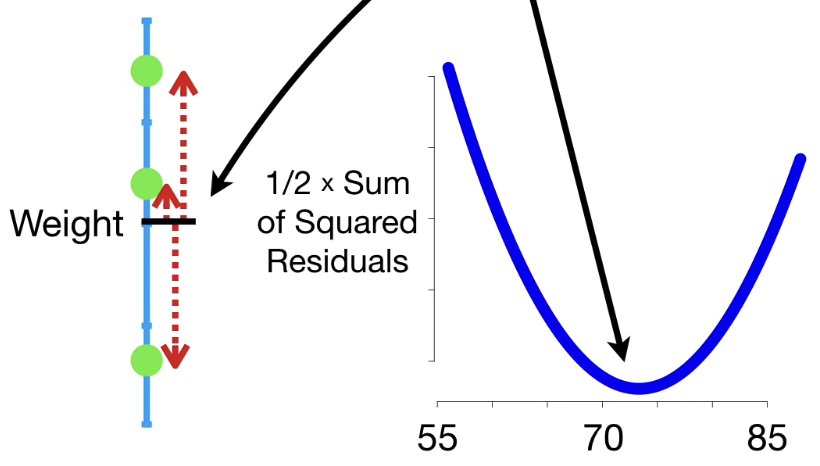
그림을 보아하니 Gradient Descent로 최소값을 찾아낼 수도 있지만, 사실 간단한 math 이니 그냥 계산해보자.
미분 값이 즉 순간변화율이 0이 되는 순간을 찾으면 된다.



구하고보니, 그냥 obeserved data의 평균값이다. 그래서 Gradient Boost model을 초기화 할 때 observed data의 평균값으로 한다. $F_o(x)$ 는 초기 예측값인 leaf라는 것을 확인했다.

m = 1
#M is usally 100
for i in range(m, M)
m 은 첫번째 tree이고, M 은 마지막 tree이다.

for i in range(1, n)
#for all samples
$\frac{\partial \textrm{ Loss function}}{\partial \textrm{ predicted}}$
즉, $-\textrm{Observed - Predicted}$ 에 - 가 붙은 형태이니 결국 $\textrm{Observed - Predicted}$ 즉, Residual이다.
$F(x) = F_{m-1}(x)$는 m = 1 일 때, $F(x) = F_0(x)$ 임을 알 수 있다.
즉, $r$ 은 Residual이고 $i$ 는 sample number 이며, $m$은 몇번째 tree인지 알려준다.
(A)는 모든 샘플의 residual을 계산한다.

(A) 과정이 Graident 를 구하는 과정이므로, Gradient Boost 라는 이름을 얻게 되었다.
그리고 Loss function은 Linear regression과 달리 $\frac{1}{2}$ 이 앞에 붙어있다. 따라서 명칭이 약간 다르다. Pseudo Residual이다.

이 말은 Residual이 terminal leaf 로 끝나는 regression tree를 만든다는 것이다. j 는 leaf 의 index이다.


$x \in R_{i,j}$ 는 i,j 번째 leaf에 존재하는 data sample 들을 뜻한다.
우변을 최소화하는 $\gamma$ 즉 residual을 찾는 것이 목표이다.
즉 미분 값이 0인, 0 = observed - (선행 예측값 + 최소화 하는 Residual) 이다.
분석하고 나니, 위에서 살펴보았던 결과와 같다.

예시로 아래와 같은 트리가 있다고 할 때,



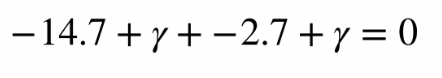

위와 같이 계산 가능하다.
정리하자면 residual은
0 = observed - (선행 예측값 + 최소화 하는 Residual)
observed - 선행 예측값 = Residual
이 되고,
같은 leaf 여러개의 residual이 존재할 경우
각 residual 의 평균이 leaf의 residual이 된다.

$\nu$ 는 learning rate이다.
새로운 예측 값 = 이전 예측값 + learning rate X 데이터 샘플이 해당되는 leaf의 residual들
우리가 흔히 Gradient Boost를 개념화 할 때 초기 예측 값 + 트리_1 leaf residual + 트리_1에 영향받은 트리_2 leaf residual + 트리_2에 영향받은 트리_3 leaf residual .... 로 구조화 하기 때문에 (D) 공식이 이해가 잘 안갈 수도 있지만, 그냥 누적 분포처럼 $F_m(x)$은 누적 값이라고 생각하면 된다.



Gradient Boost는 예측 값과 관측 값의 차이를 최소화 하는 loss function의 미분값(Gradient)에 learning rate를 곱하여 예측 값을 관측 값과 유사하게 근사하는 기법이다.
분류 모델로의 Gradient Boost
Gradient Boost가 Classification에 사용되면 Logisitic Regression과 겹치는 부분이 많다.
logisitic regression을 잘 모른다면 이 글을 읽어보자.
사용 데이터는 아래와 같다.

회귀모델과 마찬가지로 초기 initial 예측을 생성한다. 여기서는 각 개인의 log(odds)를 사용한다.
※ odds: 발생 확률/ 발생하지 않을 확률
샘플 중 Troll 2 를 좋아하는 인원은 4명이고 싫어하는 인원은 2인이므로
$\log(\textrm{odds})$ = $\log (\frac{4}{2}) = 0.7$ 이다.
Initial Prediction

Logistic Regression recall
Logistic Regression은 이진 분류의 경우, 각 분류에 속할 확률을 계산한다.


즉 이항 로지스틱 모델에 범주 정보를 모르는 입력 벡터 x를 넣으면 범주가 Positive 에 속할 확률을 알 수 있다.

정보를 활용하여 Troll 2 를 좋아할 확률을 계산해보자.
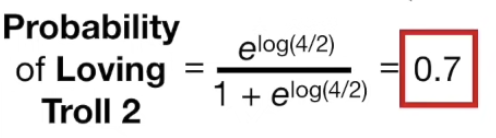
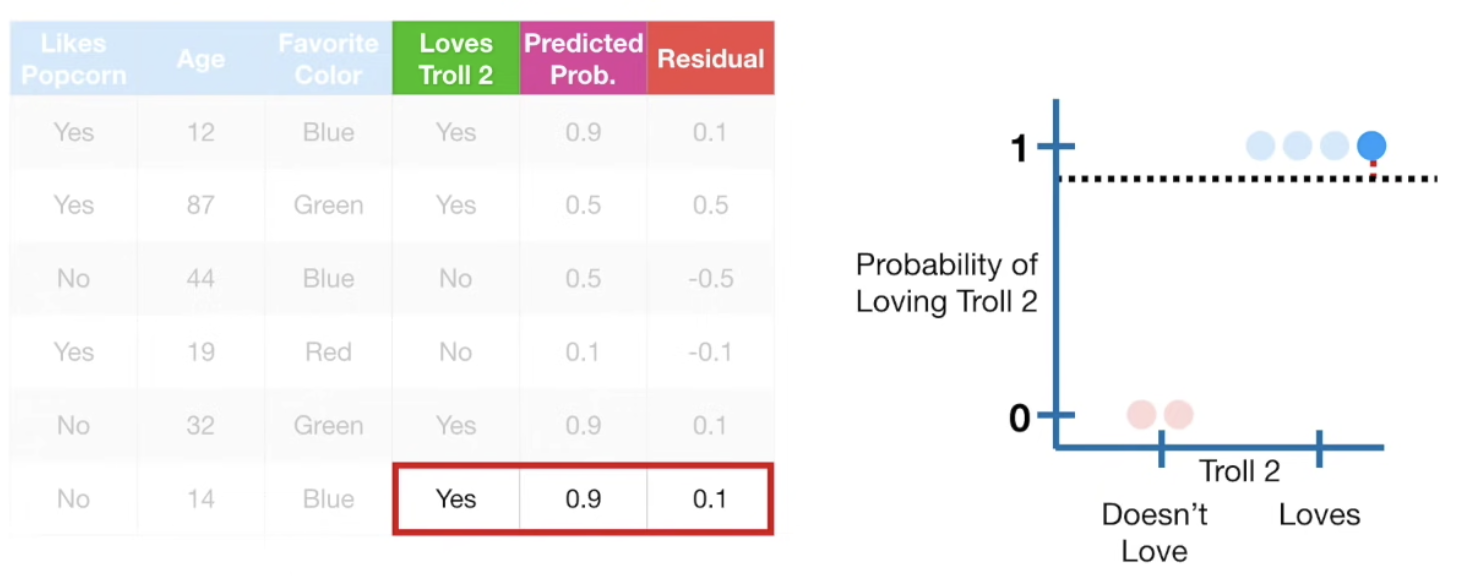
사실 정확한 확률은 아래와 같다. Troll 2 를 좋아할 확률은 4/6 = 0.6667 과 동일하다.
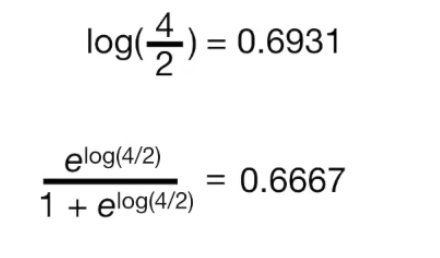
0.5를 의사결정의 threshold로 삼으면 Training Set 의 모든 샘플은 Troll 2 를 좋아한다고 예측할 수 있다.
이제 Initial Residual을 잡아보자.


※ Residual = (Observed - Predicted)
Residual을 업데이트 하기 위해 feature로 Residual을 분류하는 Tree를 생성한다.


※ 주의 사항
Gradient Boost 를 Regression에 사용할 때는 leaf 에 corresponding 되는 데이터 샘플이 1개라면 Output Value 를 계산할 때 별다른 처리 없이 residual 값 그대로 prediction 예측에 사용되었다.

그러나 Classification에 사용될 때는 initial Prediction 자체가 log(odds)인 반면, leaf 의 residual 은 확률이기에 바로 예측에 사용할 수 없고 변환을 해주어야 한다.
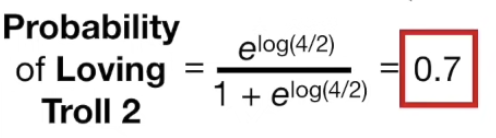

이에 따라 아래식을 활용한다. 아래 식은 아래쪽 수식 유도 과정에서 설명한다.

해당 leaf 는 데이터가 한개이므로 아래와 같이 정리할 수 있다.


처음에 모든 샘플이 1에 속할 확률이 0.7 로 사전 설정되었으므로 모두 동일하지만, update 과정에서 당연히 달라진다.

update 를 모두 마친 후, initial guess + learning rate $\times$ 각 leaf의 residual 로 새로운 prediction을 만든다.
(원할한 설명을 위해 lr 을 0.8로 잡았지만 현업에서는 보통 0.1을 사용한다.)
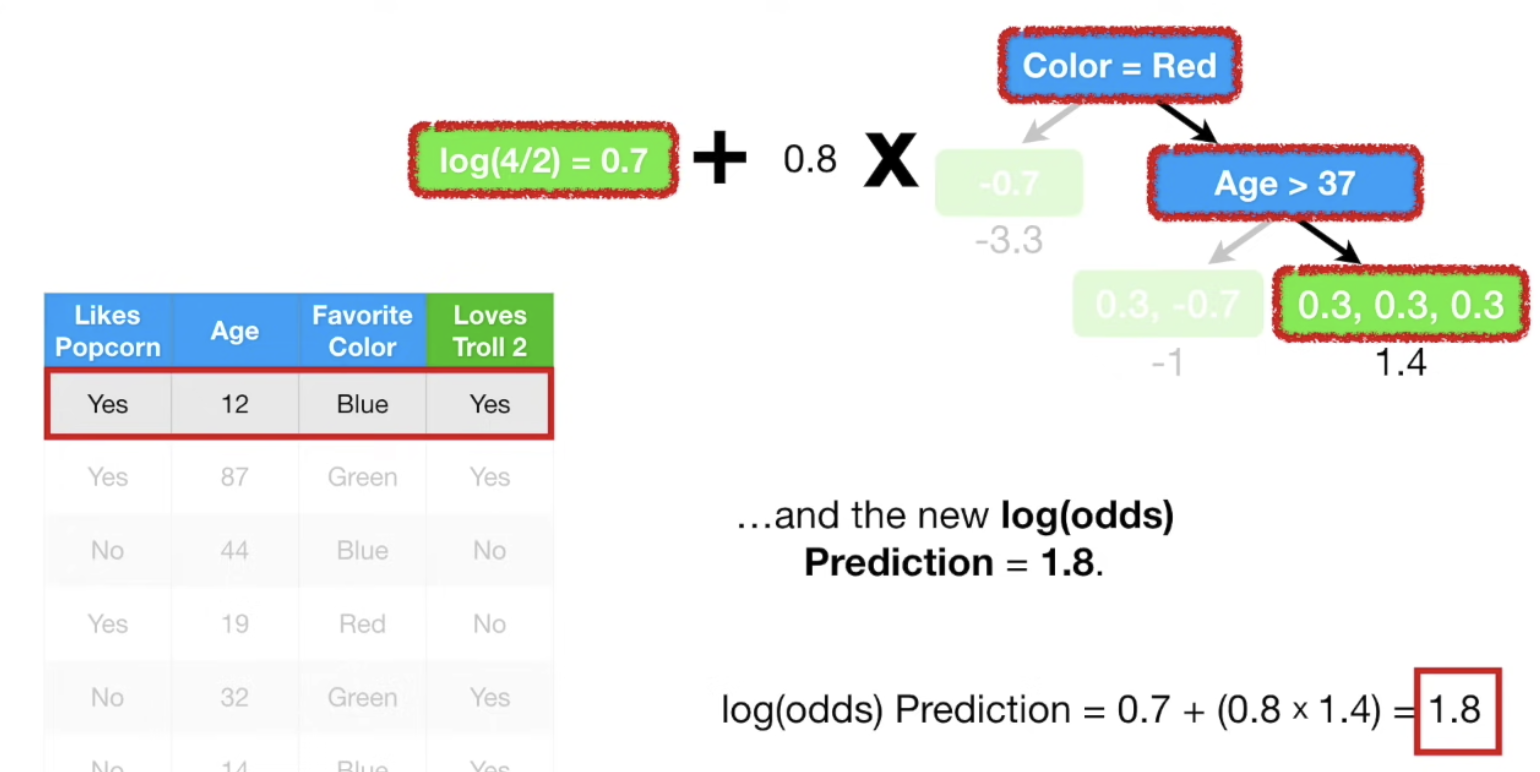
초기 예측값 log(odds) 를 먼저 업데이트하고,

Troll 2 를 좋아할 확률을 업데이트 한다.

※ 애초에 initial guess를 log(odds)로 하지 않고 확률로 하면 어떨까 싶지만, 애초에 logistic regression을 수행하는 이유가 linear 회귀 모델로 해결하지 못하는 부분에 odds 를 취하고 log 를 이용하여 decision boundary에서 변화를 급격화 시킴으써 명확하게 구분하기 위함이라는 것을 기억하자. 즉, tree가 분류를 수월하게 하기 위해서라도 log(odds) 과정은 필수이다.

Loves Troll 2 label이 Yes 임에도 probability 가 0.7에서 0.5로 떨어졌다. 즉 예측이 오히려 나빠졌다. tree를 하나만 만들지 않고 여러개 만드는 이유가 바로 여기에 있다.
지금부터는 iterate 과정이다.
새롭게 예측한 probabilty 를 이용하여 Residual을 새롭게 update한다.

업데이트 한 residual로 tree를 새롭게 생성하여 분류한 후,
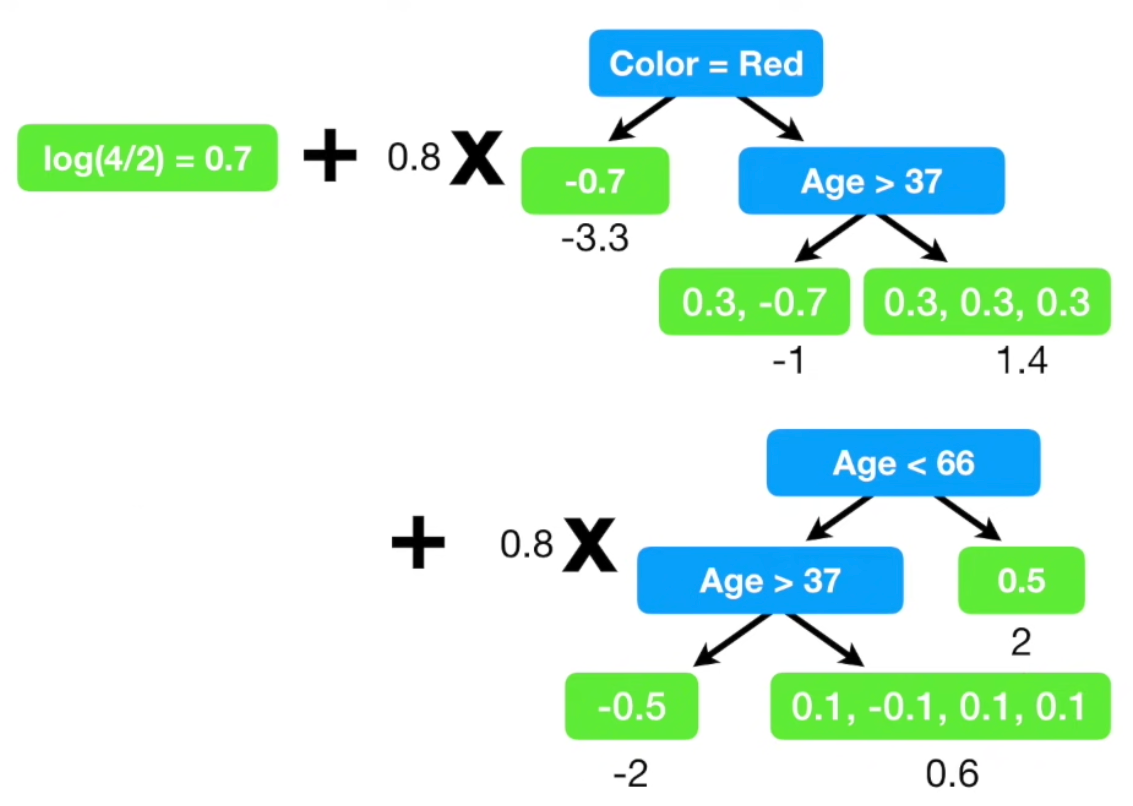
사용자가 사전 설정한 maximum 횟수, 혹은 residual이 특정 임계값 아래로 내려갈때 까지 위 과정이 iterate 된다.

학습이 완료 된 이후, input data가 주어지면 위 과정을 거쳐 Log(odds) prediction 값을 얻게 되고, 이를 통해 probability를 업데이트 한다.

Gradient Boost 이론 (Classification)
※ log(likelihood)

각 우도를 곱하는건 너무 stressful 하다.
양 변에 log 를 취해주면
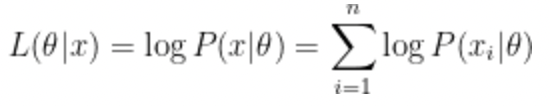
계산이 간단해진다.
우도를 모른다면 이 글을 읽어보자.
우도: 각 사건이 일어날 확률을 곱했을 때 최대가 되는 경우가 가장 일어날 확률이 높은 상황
log: log는 단조 함수이므로 log 를 취해주는 것은 문제가 없다.
설명의 간소화를 위해 sample이 3개인 데이터를 사용한다.

Likelihood는 클 수록 예측이 잘 된다는 뜻이다. 당연히 Logistic Regression의 목표도 log(likelihood)를 최대화 하는 것이다.
이에 따라 log(likelihood)를 Loss function으로 쓰려면 -1 $\times$ log(likelihood)를 사용해야 한다.

이진 분류 문제이므로, $P(x_i | \theta)$ 가 1 아니면 0 이다. 이에 따라 Loss function을 아래와 같이 정리 할 수 있다.


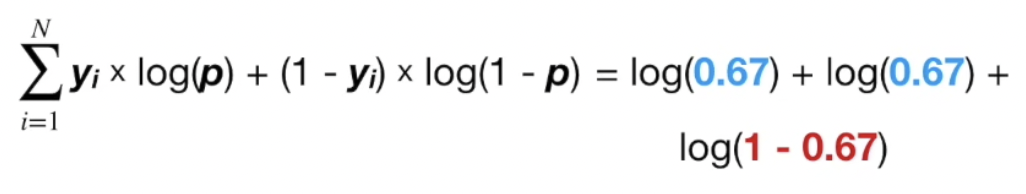
함수가 미분 가능여부를 확인하자.
미분 가능을 확인하는 과정이니, sum 은 생략한다.

$y_i$ 의 readability를 위해 Observed 로 기입

$\log(p) - \log(1-p)$ 는 $\frac{\log(p)}{\log(1-p)}$ 이므로, log(odds) 이다.
그리고 $\log(1-p) 는 -\log(1+e^{\log(\textrm{odds})})$이다. 아래 유도과정을 살펴보자.


이제 5) 가 미분 가능한지 확인해보자. 추후 우리의 목표는 prediction (log(odds)) 로 미분을 했을 때 0이 되는 극저점을 찾는 것이므로 log(odds) 로 미분가능한지 확인한다.
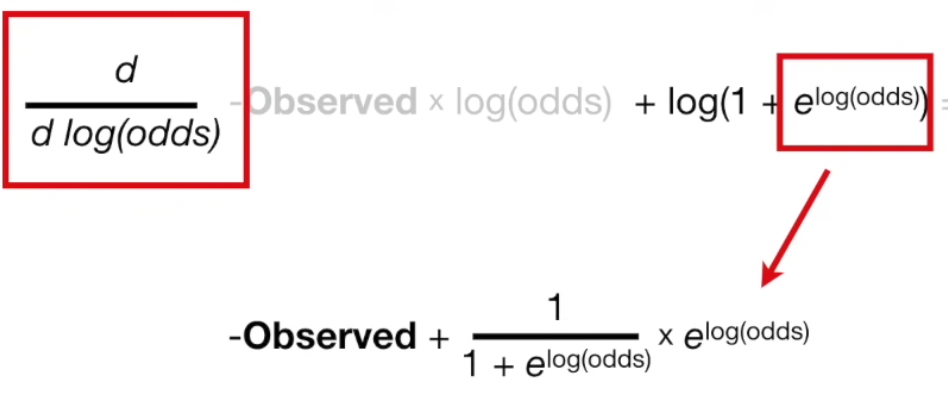
chain rule 에 의해 미분하면 아래와 같이 정리 가능하다.


미분 가능한 것을 확인했다.
Model 을 initalize 하기 위하여 initial prediction 이 필요하다.

log(odds)은 prediction 이므로 위 식은 아래와 같이 정리 가능하다.


위 값을 minimize 하는 gamma 값을 찾아야 하므로 log(odds) 로 미분한다.
위에서 미리 구해놓았던

를 활용하여

$-1 + p + -1 + p + -0 + p = 0$
$p = \frac{2}{3}$
$\log(odds) = \log(\frac{2}{1})$

Yes: 2 , No: 1 라는 점에서 위 유도과정이 reasonable 한 것을 확인했다.
$F_0(x) = \log(\frac{2}{1}) = 0.69$
initial guess 를 구했다.


m = 1
#M is usally 100
for i in range(m, M)
m 은 첫번째 tree이고, M 은 마지막 tree이다.

for i in range(1, n)
#for all samples
Loss function의 미분은 이미 계산을 완료했다.

$F(x) = F_{m-1}(x)$ 이므로,
Pseudo Residual 을 업데이트하면 아래와 같다.


Regression Tree 를 만들어서 분류한다. 단, 아래 tree가 Stump인 것은 계산의 단순화를 위해서이다.


(C) 를 통해 아래 식이 유도되는 과정을 살펴보자.

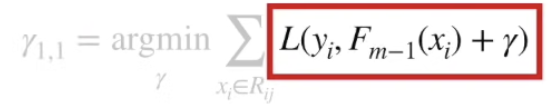
Loss function은 이미 알고있다.
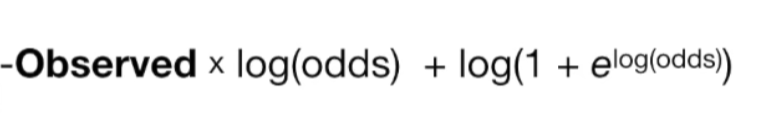

sum은 생략한다. (데이터가 한개인 경우, 계산의 단순화)

i에 1 을 대입

gamma 에 대하여 미분 값을 찾는 것이 가장 정확한 방법이나 너무 많은 연산량이 필요하다.
이에 따라 Regression을 위해 Gradient Boost 를 사용한다.
즉, 테일러 급수를 통해 Loss function 을 근사한다.

자세한 내용은 이 글의 Gradient Descent 내용을 참고하자.

$\gamma ^2$ 이하 항을 $Q(x)$ 라 할 때, $Q(x)$ 의 크기는 무시할정도로 작다고 가정하여 생략되었다.
