꺼내먹는지식 준
머신러닝 정리 7 - Decision Boundary, logistic regression, Gradient Descent 본문
머신러닝 정리 7 - Decision Boundary, logistic regression, Gradient Descent
알 수 없는 사용자 2022. 10. 28. 17:35지금까지 Traditional 한 기법인 Decision Tree, Linear Regression, Rule base 기법 등을 알아보았다.
그리고, 가장 최근 글에서는 conditional independence 를 가정한 Naive Bayes Classifier 를 알아보았다. Navie Bayes Classifier 는 MAP 기법으로 간단하게 구현된다.
하지만 Navie Bayes Classifier 는 Naive 한 가정으로 인해 feature 간의 interaction을 전혀 반영하지 못한다는 점에서 문제가 있었다.
이러한 문제를 탈피한 여러 방법론들을 앞으로 알아보려고 한다.
그 중, 가장 기본적인 것 부터 알아보자.
Logistic Regression
Logisitc Regression 도 Bayes risk (error)를 최소화 하는 형태로 구현되었다.
이글에서는 Logisitic Model 을 구현 한 후, parameter 를 optimize 하는 MLE(극점 이용) 기법을 통해 parameter $\theta$ 를 inference 하는 과정을 다루고, 마지막에 Naive Bayes 와 Logistic Regression 을 비교해본다.

위 이미지는 이미 그전 글들에서 너무 여러번 다뤘던 내용이므로 간단하게 요약만 해보자.
Binary Classification 문제에서 postive 일 확률이 0.7 이면, negative 일 확률은 0.3이다.
0.3 만큼이나 negative 가 될 bayes risk 를 안게된다. (위 그림에서는 색칠 된 영역)
위 점선으로 모델링 된 확률을 실선처럼 모델링 하여 bayes risk 자체를 최소화 하는 방법이 있다면, 그렇게 하는 것이 가장 이상적이다.
$x_m$ 을 기준으로 왼 쪽이면 y을 갖고, 오른 쪽이면 y을 갖는다. 이 $x_m$ 의 위치를 Decision Boundary 라고 부른다. Decision Boundary 를 기준으로 각 y, y 가 될 확률이 급격하게 증가하여야 이상적으로 구분되었다고 할 수 있다.
이 두가지를 만족하는 것이 위의 실선이다. 이 실선을 지금부터 S 커브 혹은 Sigmoid function 이라고 부르자.
Likelihood 를 어떤 형태로 만들어야 sigmoid 형태가 될 수 있을지 지금부터 살펴보자.
사용 데이터 셋: Credit Approval Dataset
http://archive.ics.uci.edu/ml/datasets/Credit+Approval
UCI Machine Learning Repository: Credit Approval Data Set
Credit Approval Data Set Download: Data Folder, Data Set Description Abstract: This data concerns credit card applications; good mix of attributes Data Set Characteristics: Multivariate Number of Instances: 690 Area: Financial Attribute Characteristics
archive.ics.uci.edu
- 690 Instances total
- 307 positive instance
credit card 신청인 총 690 인 중, 307 명만 허가된 데이터 셋이다.
A1 ~ A16 features
class C 에 대하여, 총 16개의 feature가 존재한다.
이 중 A 15 attribute 를 사용하여 예측을 해보자.
Y axis 는 P(Y|X) 이다. (응답 C)
Decision Boundary 는 회색 줄로 표시되었다.

왼쪽 그림은 X = A 15, Y = C 이고,
오른쪽 그림은 X = log(A15), Y = C 이다.
물론 왼쪽 그림을 보면 Decision Boundary 보다 아래에 있어도 응답이 positive인 사람들이 있지만, negative 인 사람들이 모두 Boundary 보다 아래에 있다.
X 를 linear 하게 보니 생각보다 clear 하게 보이지 않아, log 를 씌운 후 결과값을 본게 오른쪽 그림이다.
※log 를 씌운다는 것 자체가 급격한 값의 차이를 좀 누그려 뜨려서 보겠다는 것이다.
1, 10, 100, 1000 $\rightarrow$ 1, 2, 3, 4
그 결과 Boundary를 기준으로 label의 나뉘는 경향성이 비교적 잘 보인다.
A 15를 linear regression 으로 fitting 해보자. 물론 discrete 한 label을 fitting 한다는게 말은 안되지만 한번 해보자.
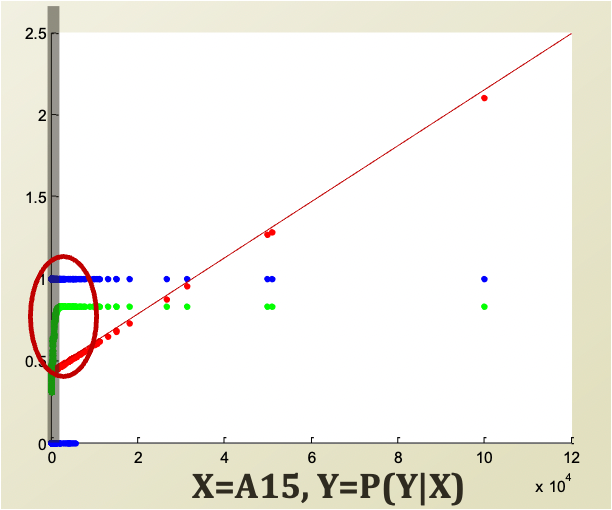

왼쪽 그림을 살펴보자. 빨간 선으로 linear 하게 fitting 이 되었다. 그리고 초록색으로 logistic regression도 해보았다. (logistic regression에 대해 아직 설명하지 않았다 뒤에서 설명한다. 다만, logistic regression 은 오른쪽 그림과 같이 S 의 형태를 띈다는 것만 알아두자.)
워낙에 데이터가 모여있어서 초록색 fitting 된 커브가 잘 눈에 안들어오지만, 동그라미 친 부분을 확대하면 오른쪽 그림과 같이 S 자 인 것을 확인할 수 있다. (오른 쪽 그림의 검은 선은 decision boundary를 임의로 표시해놓은 것이다. 원점이 아니다.)
좀 더 변화를 넓게 보기 위하여 A15 에 log 를 취해보자.

Blue = $(X, Y_{true})$
Red = $(X, P_{lin} (Y|X))$
Green = $(X, P_{log} (Y|X))$
(X가 log 가 씌어진 형태이므로, 일반적 linear 한 형태가 아니라 증가하는 형태를 띄게 되었다.)
logistic regression이 자신의 decision boundary 근처에서 부드럽고 급격하게 올라가고 그 후 그 상태를 유지하는 S 커브 형태를 만들어낸다는 것을 알 수 있다.

linear regression 은 0.5 를 지나는 지점이 logstic regression 보다 훨씬 앞지점이다.
대충 봐도 logistic regression이 사실에 근접하게 정확해 보인다.
linear regression 이 0.5 를 지난 지점 전 부분의 positive data 는 모두 에러처리가 되어버린다. (빨간 원)
반면, logistic function 에러 처리되는 부분이 훨씬 적다. (초록 원)
negative data에서도 마찬가지다.
눈으로 봐도 S 커브를 사용하는 것이 더 효율적이다.
Sigmoid
S 커브를 좀 더 전문적으로 sigmoid 형태라고 한다.

sigmoid function 이란?
- bounded 되었다.
- differentiable 하다.
- Real function 이다.
- 모든 input 에 대해서 output이 특정 boundary 내에서 정의가 되어있어야 한다.
- positive derivative 즉, 증가하는 형태여야 한다.
Logistic Function

- Logistic function 의 정의된 Y 영역을 보면 0 ~ 1 이다.
- 다른 sigmoid function들을 보면 -1 ~ 1 이라는 차이가 있다.
- 보통 국가의 경제력과 같이 정체 중에 어떤 계기로 갑자기 성장하고 다시 정체되는 상황에 많이 사용된다.
- sigmoid function 의 특징을 모두 가지고 있어서 사용하기 좋다.
- 당연히 미분도 쉽다. 그러다보니 미분하여 극점 찾기도 용이하다.
Logistic Function 의 역함수는 Logit function 이다.
$$f(x) = \log (\frac{x}{1-x})$$



logit function의 정의역 범위는 [0, 1]이다. 이에 따라 x 를 확률 값으로 보아 p 로 치환할 수 있다.
$$ f(x) = \log (\frac{x}{1-x}) \rightarrow x = log(\frac{p}{1-p})$$
또한 logistic function 은 logit function의 역함수 이므로, p가 치역이 된다.
$$x = log(\frac{p}{1-p}) \rightarrow ax+b $$
logistic function 을 classification 하고자 하는 분포에 맞춰서 fitting을 해야 한다.

fitting은 decision boundary의 위치를 이동 시키거나, 변화 과정을 압축하거나 넓힌다.
변화 과정을 압축, 넓힘: a
decision boundary 이동: b
즉, 해당 정보들을 control 하기 위한 매개변수이다.
$$\rightarrow ax+b \rightarrow X \theta$$
$\theta$ 의 첫번째 paramter 는 특정 bias 에만 움직이도록 설정하였기에 b 가 반영되고 나머지는 a 부분을 반영한다.
(이 부분이 이해가 안간다면 그 전 글들을 읽고오시면 좋습니다.)
해당 부분은 linear regression 과 생김새가 굉장히 닮았다.
이에 따라 linear regression의 방법으로 fitting을 해보자.
linear regression의 방식으로 $P(Y | X)$ 를 fitting 하려고 한다.
이때 $X\theta = \log(\frac{p}{1-p})$
X가 주어진 상황에서 Y가 될 확률을 어떻게 정의할 수 있을까?
사실상 p는 우리가 관심있는 확률값 (inference 혹은 optimization을 하고자 하는) P(Y|X) 라고 써줘도 무방하다.
$X \theta = \log(\frac{P(Y|X)}{1 - P(Y|X)})$
즉, $X \theta$ 를 통해 regression 임을 알 수 있는데, 모양을 살펴보면 logistic 한 형태임을 확인 할 수 있어서 logistic regression 임을 알 수 있다.
※ 위 작업에서 왜 굳이 logit function으로부터 logsitic function fitting을 유도할까?
f = theta * x 형태의 linear regression에서 linear function f를 근사하고 싶은 것처럼 logistic regression은 그 아래에 있는 logit 안의 p를 근사하는 과정 이라고 생각하면 된다.
Logistic Regression
Binomial, Multi-nomial 모두 가능
Bernoulli 실험을 상기해보자.
관측값 x 가 주어졌을 때,
다음의 확률을 따른다.
$P(y|x) = \mu (x)^y (1 - \mu(x))^{1-y}$
$\mu(x)$ 를 logistic function으로 모델링 해보자.
$\mu(x) = \frac{1}{1+e^{-\theta^{T} x}} = P(y = 1 | x)$
(범위가 1에 속할 확률)
위에서 살펴보았던 logistic regression의 p 값을 $\mu(x)$ 혹은 $P(y|x)$와 동일하게 놓고 regression 한다.
$-\theta^T x$ 는 그냥 $X \theta$ 이나, 한 instance에 대한 것이기에 $x \theta$ 로 표기한다.
$X \theta = \log(\frac{P(Y|X)}{ 1 - P(Y|X)})$ 이고 이 것을 다시 써보면
$P(Y|X) = \frac{e^{X\theta}}{1 + e^{X\theta}}$ 로 정리된 것이다.
학습시 X, Y는 주어졌으므로 우리가 모르는 $\theta$ 를 알아내는 방법이 logistic function 을 학습하고 paramter 를 inference 하는 과정이다.
(※추가적으로 $\frac{P(Y|X)}{ 1 - P(Y|X)})$ 형태는 Odd의 형태이기도 하다.)
Parameter $\theta$ 찾기
(이항 로지스틱 회귀의 경우)
Maximum Likelihood Estimation (MLE) of $\theta$
관측 데이터의 확률을 최대화 하는 $\theta$ 를 찾는 법
$\hat{\theta} = argmax_{\theta} P (D|\theta)$
Maximum Conditional Likelihood Estimation of $\theta$ (MCLE)
$$\hat{\theta} = argmax_{\theta} P(D|\theta) = argmax_{\theta} \prod_{1 \leq i \leq N} P(Y_i | X_i ; \theta)$$
$$= argmax_{\theta} \log(\prod_{1 \leq i \leq N} P(Y_i | X_i ; \theta))$$
$$= argmax_{\theta} \sum_{1 \leq i \leq N} \log(P (Y_i|X_i ; \theta))$$
순차적으로 살펴보자면, 각 $X_i$ 는 독립 시행이기에 곱셈으로 $argmax_{\theta}$를 구한다.
log 를 취해줌으로써 덧셈으로 연산 과정을 간소화하였다.
베르누이 모델
$$P(Y_i | X_i ; \theta) = \mu(X_i)^{Y_i} (1 - \mu(X_i))^{1-Y_i}$$
양변에 log 를 취해준다.
$$\log(P(Y_i|X_i ; \theta)) = Y_i \log(\mu (X_i)) + (1 - Y_i) \log(1 - \mu(X_i))$$
$Y_i$로 묶어준다.
$$= Y_i\{\log(\mu(X_i)) - \log(1 - \mu(X_i)) \} + \log(1 - \mu(X_i))$$
$$= Y_i \log (\frac{\mu(X_i)}{1 - \mu(X_i)}) + \log(1 - \mu(X_i))$$
※ recall
$X \theta = \log(\frac{P(Y|X)}{ 1 - P(Y|X)})$
$\mu(x) = \frac{1}{1+e^{-\theta^{T} x}}$ (분자 분모에 $e^{X \theta}$ 를 곱한다.) $= \frac{e^{X\theta}}{1 + e^{X\theta}}$
$$= Y_i X_i \theta + \log(1 - \mu(X_i)) = Y_iX_i\theta - \log(1 + e^{X_i \theta})$$
위 과정들은 연속형 숫자가 아닌 2개의 범주로 결과가 나와야 하기에 logistic regression이 필요한 것이고, 이를 적용하기 위해 최적화하여 추론할 $\theta$ 의 형태로 수식을 정리한 것이다.
$$\hat{\theta}= argmax_{\theta} \sum_{1 \leq i \leq N} \log(P (Y_i|X_i ; \theta))$$
$$ = argmax_{\theta} \sum_{1 \leq i \leq N} \{ Y_iX_i\theta - \log(1 + e^{X_i \theta}) \} $$
미분을 통해 극점을 찾아 최적화를 해보자.
$$\frac{\partial}{\partial \theta_j} \{ \sum_{1 \leq i \leq N} \{ Y_iX_i\theta - \log(1 + e^{X_i \theta}) \}$$
$$ = \{ \sum_{1 \leq i \leq N} Y_i X_{i,j}\} + \{ \sum_{1 \leq i \leq N} -\frac{1}{1+e^{X_i\theta}} \times e^{X_i \theta} \times X_{i,j} \}$$
$\theta$ 의 개별 element 로 미분을 취하기에 X 도 $X_{i,j}$ 로 표기한다. 즉 $\theta_j$가 역할을 하는 term에 대해서만 미분이 가능 하기에 $X_{i,j}$는 $\theta_j$와 연결된 X tern만 살린다. $X_i$가 $\theta_j$와 연결된 term이면 1, 아니면 0을 대입하여 수식을 이해하면 된다.
$\log(1+e^{X_i \theta})$ 의 미분은 log 의 합성 함수, $e^{x_i \theta}$ 에서 합성함수이므로 정리하면 $ \frac{1}{1+e^{X_i \theta}} \times e^{X_i \theta} \times X_{i,j}$ 이다.
$$= \sum_{1 \leq i \leq N} X_{i,j} (Y_i - \frac{e^{X_i \theta}}{1 + e^{X_i \theta}}) = \sum_{1\leq i \leq N} X_{i,j}(Y_i - P(Y_i = 1|X_i ; \theta)) = 0$$
문제는 미분을 통해 $\hat{\theta} = $ 의 형태가 깔끔하게 딱 떨어지지 않는다.
즉, 이 방식을 통해 $\theta$ 를 closed form solution 을 구하는 것이 굉장히 어렵다.
이에 따라 open form solution 인 즉, approximation (근사)를 해야하는 형태로 나오게 되었다.
$\theta$ 의 잘 fitting 된 값을 구하기 위해 근사를 해보자.
※ recall
logistic regression 은 regression 을 통해 classification 즉 범주형 문제에서 사용하는 모델이다.
$\theta$ 의 근사법으로 딥러닝에서 잘 알려진 gradient descent 가 등장한다.
Gradient Descent
Taylor Expansion
Taylor series 는 하나의 함수에 대한 표현이다.
테일러 급수에 관한 내용은 아래 글을 참고하자.
자세한 내용은 생략하나, 다루기 어렵거나 잘 모르는 함수를 다루기 쉽고 이해하기 쉬운 다항함수로 근사하기 위해 사용한다는 점 정도만 알아두자.
https://darkpgmr.tistory.com/59
테일러 급수의 이해와 활용 (Taylor series)
테일러 급수(Taylor series)에 대한 내용은 이미 인터넷에 좋은 글들이 많습니다. 그럼에도 이렇게 다시 글을 쓰는 이유는 스스로도 애매한 부분이 많기 때문입니다. 그래서 공부하는 셈치고 관련
darkpgmr.tistory.com
Taylor series
$$f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + ... + $$
$$= \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^n$$
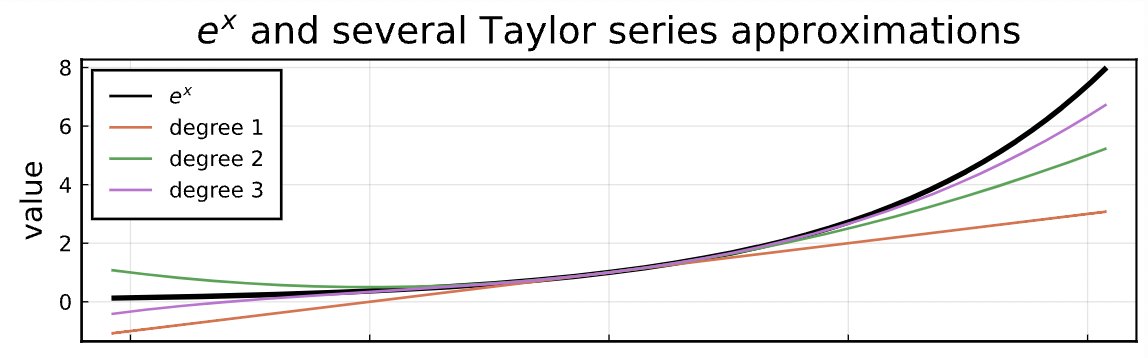
a 가 0 일 때, $e^x$ 함수를 표현해보자.
$$e^x = 1 + \frac{e^0}{1!}(x-0)^1 + \frac{e^0}{2!}(x-0)^2 + ...$$
(1 은 0차항이라서 1이 된 것이다. 사실은 같은 형태)
n 의 차원에 따라 근사도가 달라진다.
log function 은 아래와 같이 근사된다.

즉, taylor expansion(확장)으로 만약 무한대 합을 볼 수 있는 가정 하에서는 원하는 함수를 동일하게 근사할 수 있다.
taylor expansion 이 가능한 경우
infinitely differentiable 한데, real 혹은 complex number 로 만들어질 때
이 Taylor Expansion 으로 gradient descent 알고리즘을 정의해볼 수 있다.
Gradient Descent, Ascent
- 미분 가능한 함수 f(x) 가 주어지고, 초기 파라미터 $x_1$ 이 주어져야 한다. (여기서 $x_1$ 은 파라미터들의 초기 값이라는 뜻 벡터의 첫번째 값이 아니다.)
- 파라미터를 반복적으로 f(x) 를 더 크게 하는 쪽 혹은 더 작게 하는 쪽으로 이동시킨다.
- f(x) 를 음 혹은 양의 방향의 기울기로 이끈다.
딥러닝에서 워낙 여러번 정리 했던 내용이기에 부담은 없다.
방향과 속력이 중요하다.
$f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + O(\big\rvert |x-a| \big\lvert^2)$
여기서 Big-Oh notation 이 등장한 이유는 다음과 같다.
Big-Oh notation: x가 a에 가까워질 때, f(x)가 어떤 양수 M과 함수 g(x)에 의해 제한될 때를 의미한다. 이를 $ f(x)=O(g(x))$ 로 나타내고, 식으로 정의를 표현하면, $|f(x)| \leq Mg(x) $ for $ x \rightarrow a$ 로 나타낸다.
해당 함수에서는 3 제곱 이후 영향력이 작아지기 때문에 x 가 a에 가까워질 때, $\big\rvert |x-a| \big\lvert^2$ 안에 제한될 수 있는 것이다.
보통 여러 값들을 Big-oh notation의 g(x) 로 사용 가능하지만, 가장 간단하거나 tight 한 값을 사용한다.
taylor 급수는 특정한 지점 a 에 대한 deriviative 를 알 수 있어야 한다.
$a = x_i$ 로 초기값을 잡는다.
$x = x_1 + hu$, $u$ 는 unit direction vector 로 즉 특정한 속력 h 를 가지고서 특정 u 방향으로 진행해 나가는 것이 gradient descent 의 핵심이다.
h 는 learning rate 라 사람이 manual 하게 정한다. 사실 정말 중요한 건 u 이다. 일단 방향이 맞아야 한다. 이 u 는 어떻게 정할까?
$f(x_1 + hu) = f(x_1) + hf'(x_1)u + h^2 O(1)$
($a = x_1, x-a = hu$, 3번째 항은 unit vector 의 제곱을 제외한 $h^2$ 만 살아남았다.)
$f(x_1 + hu) - f(x_1) \approx hf'(x_1)u$
$h^2 O(1)$ 여기서 h 즉, learning rate 는 주로 굉장히 작다. 굉장히 작은 h의 제곱 수는 더 작다. 이에 따라 해당 값은 무시한 후 $\approx $ 처리가 가능하다.
$$u^* = argmin_u \{ f(x_1 + hu) - f(x_1) \} = argmin_u hf'(x)u = - \frac{f'(x_1)}{|f'(x)|}$$
해당 함수는 f function 을 한번 움직였을 때 감소 값을 최대화 해서 이동시키는 것이 목표이다.
$f(x_1 + hu) - f(x_1)$ 값이 최소가 되도록 하는 $u$ 를 찾는 것이 목표이다. 위에서 근사한 값인 $hf'(x_1)u$ 대입한다. 여기서 확인할 수 있는 $h f'(x) u$ 가 바로 우리의 눈에 익숙한 gradient descent 의 편미분과 방향 벡터, learning rate 의 관계이다.
u는 단위벡터이기 때문에 크기가 1이라는 사실을 알고 있다. 이때, $h f'(x_1)u$ 를 최소화를 어떻게 할까? h는 일단, 상수이기 때문에 아무런 영향을 주지 못하고 오직 u에 의해서 결정된다.
그렇다면, u 값을 통해 $h f'(x_1)u$ 를 최소화 해야 한다. 이는 둘의 방향이 180도가 되면 된다. 즉, 내적의 값이 최소가 되도록 180도의 방향을 만들어주면 된다. 그러면 u의 값은 방향만 정 반대이고 크기는 동일한 $-f'(x_1)$이 된다. 하지만, u는 단위벡터로 크기가 1이니 $|f'(x_1)|$으로 나누어주면 주어진 $u* = -f'(x_1)/|f'(x_1)|$ 이 된다. (크기만 나눔으로써 방향만 유지)
이를 좀 더 수식적으로 자세히 설명해본다면 아래와 같다.
$f(x_1 + hu) \leq f(x_1)$ $\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{|a|} \overrightarrow{|b|} \cos{a}$
이 글을 읽는 사람들이라면 이미 익숙하겠지만 당연히 $\overrightarrow{|a|} \overrightarrow{|b|} \cos{a}$ 는 내적이다.
$\cos $ 은 1에서 극대화 되고 -1 일 때 극소화 된다. 즉 -1 이 되는 180 도 지점, 기존 derivative 방향과 정 반대 방향이어야 한다. 이에 따라 $u* = -f'(x_1)/|f'(x_1)|$ 이 된다.

이제 이동 방향은 정해져 있고, 이동 속력은 우리가 정하면 된다.
결과적으로 아래와 같은 식을 얻을 수 있다.
$x_{t+1} = x_t + hu^* = x_t - h f'(x_1)/|f'(x_1)|$
직관적이어서 한번도 궁금해 하지 않았던 gradient descent 는 사실 taylor 확장으로부터 유도될 수 있었던 것이었다. (여기서 h 는 learning rate )
※ learning rate 는 step size 라고 하기도 한다.
이와 관련하여 좀 더 자세한 내용이 궁금하면 아래 글을 읽어보면 좋다.
해당 글의 내용에 gradient descent 내용까지 잘 정리되어 있다.
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
경사하강법(gradient descent) - 공돌이의 수학정리노트
angeloyeo.github.io
또한 아래 글은 gradient descent 의 실제 적용 사례를 정리한 글이다. 위 글의 내용들이 정리 된 부분도 있다.
https://itforfun.tistory.com/250
머신 러닝 정리 6.5 - Gradient Descent 가 정말 잘 동작할까?
Gradient Descent 에 대해 이론적으로 살펴볼 기회는 정말 많다. 하지만, 이게 정말 잘 동작하는지 눈으로 직접 비교하며 확인할 기회는 잘 없다. 그런 의미에서 간단하게 정리해놓는다. 본 내용은 모
itforfun.tistory.com
결론적으로 unit direction vector X stepsize(learning rate) 로 점을 업데이트 한다.
이제 logistic regression 으로 돌아오자.
미분을 통해 극점을 통해 closed form 을 찾으려던 시도는 실패였다.
이에 따라 gradient descent 를 통해 해결하고자 한다.
(실제 실생활의 많은 모델들은 closed form 으로 찾기 어렵다. 또한 미분 계수를 구하기보다는 비교적 구현이 쉬운 gradient descent 를 택할 일이 많다.)
$$\hat{\theta} = argmax_{\theta} \sum_{1 \leq i \leq N} \log(P(Y_i | X_i ; \theta))$$
여기서는 gradient descent 가 아니라 gradient ascent 이다.
$P(Y_i | X_i ; \theta)$ 의 값을 키우면 된다.
즉, $u = + \frac{f'(x_1)}{|f'(x_1)|}$ 가 된다.
- 초기 parameter $\theta$ 의 값을 결정한다.
- 반복적으로 $\theta_t$ 를 이동시켜 더 높은 $f(\theta_t)$ 값을 얻는다.
$$f(\theta) = \sum_{1 \leq i \leq N} \log(P(Y_i | X_i ; \theta))$$
$$\frac{\partial f(\theta)}{\partial \theta_j} = \frac{\partial}{\partial \theta_j} \{ \sum_{1 \leq i \leq N} \log(P(Y_i | X_i ; \theta))\} = \sum_{1 \leq i \leq N} X_{i,j} (Y_i - P(y=1 | x ; \theta))$$
편미분 과정은 위에 자세하게 나와있으므로 참고
$f'(x)$ 를 이미 알고 있으므로 경사 상승법을 적용해보자.
$$x_{t+1} = x_t + hu^* = x_t + h \frac{f'(x_t)}{|f'(x_t)|}$$
$$\theta_j^{t+1} \leftarrow \theta_j^t + h \frac{\partial f(\theta^t)}{\partial \theta^t_j}$$
$$\theta^t_j + h \{ \sum_{1 \leq i \leq N} X_{i,j} (Y_i - P(Y=1 | X_i ; \theta^t)) \}$$
$$ = \theta^t_j + \frac{h}{C} \{ \sum_{1 \leq i \leq N} X_{i,j} \bigg( Y_i - \frac{e^{X_i\theta^t}}{1+e^{X_i \theta^t}} \bigg) \}$$
C: C 는 unit vector 로 normalize 하는 값 (h 값이 작기때문에 없어도 큰 영향력이 없기도 하다.)
$\theta^0_j 의 초기값은 임의로 선택하면 된다.$
여기까지 Logistic Regression 에서 최적 해를 구하기 위한 방법인 gradient descent 가 무엇인지, 왜 gradient descent를 해야하는 이유와, 그리고 어떻게 하는지 알아보았다.
하지만 사실 Gradient descent 미분을 통해 closed form을 쉽게 찾을 수 있는 경우에도 사용 되곤 한다.
왜일까?
Revisit Linear Regression
linear regression 의 최적 parameter $\theta$ 는 아래와 같은 것을 확인했었다.
$\theta = (X^T X)^{-1} X^T Y$
closed form 으로 구할 수 있어 간단하지만, 문제는 데이터셋의 크기가 너무 커지면 적용하기 어렵다는 것이다.
dimension 이 큰 X 의 역행렬을 구하는 것도 어렵지만, 큰 X 와 큰 Y 의 matrix multiplication 을 하는 것도 쉽지 않아진다.
그렇기에 큰 규모의 linear regression 을 할 때는 $\theta$ 를 approximation 한다.
워낙 수식도 간단하고, 편미분 과정도 위에서 충분히 언급했으므로 생략한다.

'AI > 머신러닝' 카테고리의 다른 글
| 머신러닝 정리 8.5(2) - Naive Bayes는 Generative Model (0) | 2022.11.01 |
|---|---|
| 머신러닝 정리 8.5(1) - Discriminative model vs Generative Model (2) | 2022.10.31 |
| 머신 러닝 정리 7.5 - Gradient Descent 가 정말 잘 동작할까? (0) | 2022.10.28 |
| 머신 러닝 정리 6 - Naive Bayes Classifier (conditional Independence 조건부 독립) (0) | 2022.10.17 |
| 머신 러닝 정리 5 - Linear Regression (0) | 2022.10.06 |




