꺼내먹는지식 준
머신 러닝 정리 6 - Naive Bayes Classifier (conditional Independence 조건부 독립) 본문
머신 러닝 정리 6 - Naive Bayes Classifier (conditional Independence 조건부 독립)
알 수 없는 사용자 2022. 10. 17. 21:57Optimal Classification Concept
Navie Bayes classifier
Supervised Learning
supervised learning: 데이터와 레이블이 주어진 상태에서 학습을 진행
많은 경우 데이터와 동시에 레이블이 주어진다. 이 경우 레이블이 존재하므로 마치 주입식 학습처럼 데이터에 따른 레이블의 대세를 학습한다고 이해하면 좋다.
보통 Classificaion 과 Regression 문제로 많이 나뉘는데, 현재 linear regression 을 한번 다루기도 했고 보통 classificaion 을 할줄 알면 regression은 따라오므로 본글은 classification을 위주로 내용이 전개된다.
Optimal Classification
Classificaion: X (데이터) 가 주어졌을 때 적절한 y 값을 예측 (아래의 예시를 살펴보자)

X라는 정보가 조건으로 주어졌을 때, 초록 y 일지, 빨간 y 일지 예측하는 것이 (class가 2개인) classificaion 이다.
X 의 관측 값에 따라 빨간 y 일지 초록 y 일지에 대한 확률을 얻게 되는데 이 때 더 확률이 높은 쪽으로 분류하여 y 값을 결정한다.
$\rightarrow$ pdf 가 주어진다면 확률을 얻기 쉬워져 분류가 간단해진다.
pdf 를 어떻게 정의할 수 있을까?
Optimal predictor of Bayes classifier
$f^* = argmin_f P(f(X) \neq Y)$
$\hat{Y}$ 과 $Y$ 를 최소로 하는 $f^*$ 를 찾아내는 것이 바로 최적화 과정이다. 즉 바로 머신러닝의 목적인 가장 현실과 유사한 함수를 근사하여 optimal predictor 를 생성한다.
$f^* = argmax_{Y-y} P(Y = y | X = x)$
다시 말하자면, 주어진 $x$에 대하여 y 값이 최대화 되도록 하는 함수이다.
※ recall
아래는 이항 분포에 대한 MLE, MAP 이다.
MLE
$\hat{\theta} = argmax_{\theta} P(D|\theta)$
위 식을 오해하면 안된다. 최고값 $\theta$ 가 주어졌을 때 D(관측값) 가 등장할 확률을 구하는 것이 아니라,
주어진 파라미터 (특정 분포)에서 관측값이 등장할 확률인 "likelihood 값"이 최대가 되는 즉, $\theta$값을 조정해가며 관측값이 주어졌을 때, 해당 관측이 등장할 확률이 최대가 되는 순간이 바로 MLE 이다.
즉 $P(D| \theta)$ 값을 최대로 하는 $\hat{\theta}$
$$P(D| \theta) = \theta^{a_H} (1 - \theta)^{a_{\tau}}$$
$$\hat{\theta} = \frac{a_H}{a_H + a_{\tau}}$$
위 공식이 이해가 안되면 아래 첨부된 MLE 정리 글을 읽고오자.
MAP
$$ \hat{\theta} = argmax_{\theta} P(\theta | D)$$
위 식의 의미는 Maximum a posteriori 즉, 사후 분포에서 최고점의 값이므로, 사후분포에 $argmax$ 가 붙어있다고 이해하면 된다.
$$ P(\theta | D)\propto \theta^{a_{H}} (1 - \theta)^{a_{\tau}} \theta^{\alpha - 1} (1-\theta)^{\beta -1}$$
$$\hat{\theta} = \frac{a_{H}+\alpha -1}{a_{H} + \alpha + a_{\tau} + \beta - 2}$$
위 공식이 이해가 안되면 아래 MAP 정리 글을 읽고오자.
https://itforfun.tistory.com/242
머신 러닝 정리 1 - MLE, MAP 정리
베이즈는 이미 2번 정리를 했지만, 여러번 볼 수록 좋기에 한번 더 정리를 한다. Supervised Learning Unsupervised Learning Label이 있는 learning (분류, regression) label 없이 주어진 데이터로 패턴 파악(cl..
itforfun.tistory.com
MLE, MAP 를 이용한 Optimal Classification and Bayes Risk

2가지 클래스로 분류하기 위해 다음과 같은 pdf 가 있다고 하자. pdf 는 점선으로도, 실선으로도 표현이 가능하다. (추가적인 설명은 추후 기술된다.)
pdf 위의 한점 $x_1$ 에 대한 $p1, p2$는 더하면 1이 된다. (y, y 중 하나로 분류되어야 하므로)
해당 그래프에서 특이한 점은 파란점 $x_m$ 이다. 정확하게 0.5 로 나누어 떨어져 어느 한쪽으로 분류할 수 없다.
해당 지점을 decision boundary라 한다.
아무래도 점선, 실선 중에서 '분류의 측면'에서 봤을 때 실선이 다음의 이유로 효용성이 높다.
- 점선에 비해 실선이 더욱 큰 확률 차이로 클래스를 구분한다.
- decision boundary를 기준으로 더욱 급격한 경사로 두 클래스를 명확하게 구분한다.
분류 과업은 조금이라도 확률이 더 높은 것을 선택한다. 즉, decision boundary 를 기준으로 왼쪽인 y 로 분류했다고 할 때 왼쪽에 존재하는 빨간색 영역은 error 이다.
이러다보니 점선보다 실선의 경우 error 영역이 (아래 표시된 영역 만큼) 더 작으므로 실선을 선택하는 것이 더 유익하다.
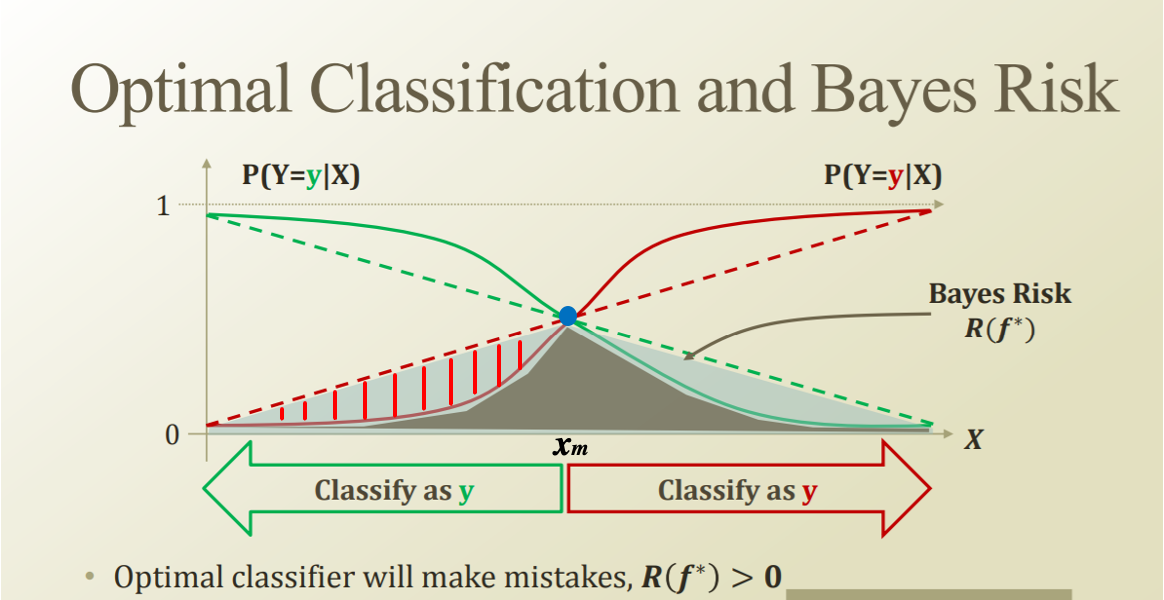
error 영역을 bayes risk 라 한다.
위 내용으로 살펴봤을 때, optimal classifier 는 bayes risk 이라고 불리는 error 영역을 줄이는 것을 목표로 한다.
즉, error 영역을 줄이기 위해 linear 한 pdf를 어떻게든 S 커브 형태로 만들려고 한다.
가장 대표적인 것은 우리가 잘 아는 logistic function 이다.
logistic function을 직접적으로 다루기 전에 좀 더 개념 이해에 초점을 맞춰서 살펴보자.
먼저 주어진 데이터만을 가지고서 확률을 이용해서 위와 같은 S 커브 만들어보고, 커브가 classifier 의 성능을 어떻게 높히고 있는지 보자.
$f^* = argmax_{Y=y} P(Y = y | X = x)$
위 공식은 데이터에서 주어진 Y 와 예측한 y 가 최대한 같은 값이 되는 확률을 만드는 근사 함수를 뜻한다.
이 공식은 bayes theorem 을 이용하여 아래와 같이 정리할 수 있다.
$= argmax_{Y=y} P(X = x | Y = y) P(Y = y)$
$P(Y = y)$ : Class Prior = Prior
문제는 Likelihood 경우 $x$ 변수의 개수에 따라 계산이 복잡해진다.
예를 들어 키에 따른 여자 친구 유무의 경우 처리가 변수가 1개여서 간단하지만,
키, 나이, 재산, 지역, 종교 등 변수의 개수가 여러개일 때는 각 변수의 interaction이 복잡할 수 있어 이 때는 likelihood 계산이 어렵다.
이에 따라 Navie Bayes classifier 이 제안되었다.
Navie Bayes classifier

주어진 X(날씨정보)를 통해 Y(외출 여부)를 판별하는 과업이 있다고 가정하자.
$f^* = argmax_{Y=y} P(X=x|Y=y)P(Y=y)$
위 식은 $f^* = argmax_{Y=y} P(Y=y | X=x)$ 를 bayes therom 으로 정리한 것이다.
위 정리한 식이 실제 사례에 적용 가능한지 확인해보자.
$P(X=x | Y=y)$
$= P(x_1 = \textrm{sunny}, x_2 \textrm{warm}, x_3 = \textrm{normal}, x_4 = \textrm{strong}, x_5 = \textrm{warm}, x_6 = \textrm{same} | y=\textrm{Yes})$
$P(Y=y) = (y = \textrm{Yes})$
Prior 는 구하기 쉽다.
Yes: $\frac{3}{4}$
No : $\frac{1}{4}$
그러나 class conditional density 인 likelihood 의 계산은 좀 복잡하다.
위에서 잠시 언급했지만 class conditional density를 계산하기 위하여 몇개의 parameters 가 필요할까? 그리고 몇개의 관측치가 필요할까?
Prior 는 $P(Y=y) \,\, \textrm{for all y})$ 로 (클래스 개수 - 1) 즉 여기서는 1개의 parameter 만 필요하다.
하지만 $P(X=x | Y=y) \,\, \textrm{for all x,y}$ 는 각 $x_i$ 마다 2개의 선택지만 있다고 해도 $(2^4 - 1)$ * class 개수 (k개) 만큼이나 필요하다. 실제로 좀 더 복잡해지는 상황에서는 사용이 불가능하다.
$f^* = argmax_{Y=y} P(X=x|Y=y)P(Y=y)$
현실 세계를 근사한 다음의 함수는 parameter의 수가 많다보니 현실세계를 잘 반영하기 위해서는 아주 큰 데이터가 필요하다.
즉, 위 함수(joint probability distribution) 를 어떻게든 조정을 해야만 한다.
문제 구간은 다음과 같다.
$P(X=x | Y=y) \,\, \textrm{for all x,y} \rightarrow (2^d -1)k$
당연히 귀중한 data를 줄이는 것은 고려사항이 아니다. (데이터의 귀함)
파라미터 개수에 대한 보충 설명
https://itforfun.tistory.com/254
머신러닝 정리 7.5(2) - Naive Bayes는 Generative Model
Naive Bayes 가 Generative model 인 것을 확인하기 위하여 이전 글 에서 Generative Model에 대한 간략한 소개글을 작성했다. 해당 글을 원할하게 읽기 위해서는 이전 글을 간단하게 살펴보는 것을 추천한다.
itforfun.tistory.com
Conditional Independence
X 의 각 feature 들이 독립적이라고 가정 하여 연산 수를 줄이는 방법이다.
$P(X = < x_1, ... , x_i> | Y =y) \rightarrow \prod_i P(X_i = x_i | Y = y)$
예를 들어 여자친구가 입고오는 옷을 class variable 이라고 가정해보자. 이 때 X 는 키, 몸무게, 그날의 기분, 옷의 불편도라 하자.
여자친구는 기분이 별로면 편한 옷을 입고 오는 경향이 있다. 이 말인 즉슨, 기분과 옷의 불편도는 높은 상관관계가 있다는 뜻이다.
즉 독립이라 가정하는 것이 실제 상황에서는 어렵다. 그럼에도 불구하고 직접 계산하는 것은 $2^d - 1$ 만큼의 계산이 필요하기에 억지스럽고 naive 하게 가정하여 처리하는 것이 naive bayse classifier 이다.
conditional independence는 아래와 같이 표기한다.
$( \forall x_1, x_2, y) $. $P(x_1|x_2, y) = P(x_1|y)$
$x_2$ 가 주어져도 주어지지 않은 것과 확률이 같다.
$P(x_1, x_2|y) = P(x_1|y) P(x_2|y)$
위와 같이도 적을 수 있다. 우리에게 좀 더 익숙한 표기이다.
예를들면 아래와 같다.
$P(\textrm{Thunder|Rain, Lightning}) = P(Thunder|Lightening) $
Conditional 와 Marginal Independece 차이
각 independence 를 설명하기 전에 각 conditional, marginal probability 가 뭔지 간단하게 살펴보자.
Marginal Distribution 은 이전 글에서 언급한 주변 확률 분포이므로 사실 글을 읽고 아래부분을 스킵하고 넘어가도 된다.
다음 3개의 binary random 변수가 있다고 가정하자. P (H,S,F)
- $H (심장병) \,\, \textrm{domain}(H) = {h, \neg h}$
- $S (담배) \,\, \textrm{domain}(H) = {s, \neg s}$
- $F (비만) \,\, \textrm{domain}(H) = {f, \neg f}$
각 조건에 따른 확률이 아래와 같을 때

Marginalization 은 아래와 같다.
$$P(H,S) = \sum_{x \in \textrm{domain}(F)} P(H,S,F = x)$$
$$P(H) = \sum_{x \in \textrm{domain}(S, F)} P(H,S = y, F = x) $$
$$P(S) = \sum_{x \in \textrm{domain}(H, F)} P(H = z,S, F = x) $$

반면에 conditional probability 는
$$P(S|H) = \frac{P(S,H)}{P(H)}$$
즉, H 가 일어났다고 가정하기에 그냥 $P(S,H)$ 와는 차이가 있다.

또한 H 가 일어났을 때, S 의 경우는 일어나거나 안 일어나거나이므로, 합쳐서 값이 1 이다.
아래 chain rule 을 살펴보면 흥미로운 사실을 알 수 있다.
$$P(H,S,F) = P(H) \times P(S|H) \times P(F| H,S) $$
$$= P(H) \times \frac{P(S,H)}{P(H)} \times \frac{P(S,H,F)}{ P(S,H)}$$
약분 되어 $P(S,H,F)$ 만 남는 것을 볼 수 있다.
베이즈 정리도 살펴보자.
$$P(S|H) = \frac{P(S,H)}{P(H)}, \,\, P(H|S) = \frac{P(S,H)}{P(S)} $$
위 식에서 두번째 식을 다시 쓰면
$$P(H|S) \times P(S) = P(S,H)$$
해당 식을 위의 첫번째 식에 대입하면 아래와 같이 정리된다.
$$P(S|H) = \frac{P(H|S) P(S)} {P(H)}$$
Marginal Independence
Y 값 에 대한 정보가 X 값에 대한 믿음에 영향을 전혀 끼치지 않는 경우에 우리는 랜덤 변수 X 가 랜덤 변수 Y에 대해 marignal independence 하다고 말한다.
간단하게 아래와 같이 적을 수 있다.
$$\textrm{if, for all } x_i \in dom(X), y_k \in dom(Y), P(X= x_i | Y = y_k) = P(X= x_i) $$
그리고 이건 아래와 같이 정리될 수 있다.
$$P(X) = P(X|Y) = \frac{P(X,Y)}{P(Y)}$$
이는 또 아래와 같이 정리될 수 있다.
1)
$$P(X) \times P(Y) = \frac{P(X,Y)}{P(Y)} \times P(Y)$$
$$P(X)P(Y) = P(X,Y)$$
2)
$$P(X) \times P(Y) \times \frac{1}{P(X)} = \frac{P(X,Y)}{P(Y)} \times \frac{1}{P(X)} \times P(Y)$$
$$P(Y|X) = P(Y)$$
2번식을 참고해서 실제 예시를 들어보자.
$$P(치통, 검진, 충치, 날씨) = P(치통, 검진, 충치) P(날씨)$$
아까 잠시 살펴보았던 심장병, 담배 예시를 살펴보자.

P(S) 와 P(S|H) 결과 값이 다르므로 서로 marginally independece 하지 않다.
한마디로 marginal independence는 우리가 평상시에 생각하는 독립이다.
Conditional Independence
그러나 위에서 살펴봤듯이 marginal independence는 $O(2^n)$ 의 복잡도를 가진다.
이에 따라 좀더 약한 독립 가정인 conditional independence 를 사용한다 .
아래의 예시를 살펴보자.
P(치통, 충치, 검진 성공)

충치와 검진 성공이 marginally independent 하지는 않다.
그러나 만약 내가 충치를 가지고 있다 할 때, 내가 치통의 유무에 따라 검진 성공 여부가 달라질까? 그렇지 않다.
1) $P(검진성공 | 치통, 충치) = P(검진성공 | 충치)$
만약 충치가 없다해도 마찬가지이다.
2) $P(검진성공 | 치통, \neg 충치) = P(검진성공 | \neg 충치)$
치통이나 검진성공여부는 충치가 있을 때 둘다 일어나는 일이지만, 치통과 검진성공 여부는 서로 직접적인 영향이 없다.
즉, 충치라는 상태가 주어졌을 때 검진의 성공 여부는 치통과 conditionally independent 하다.
$$P(\textrm{검진성공 | 치통, 충치}) = P(\textrm{검진성공 | 충치})$$
$$P(\textrm{치통 | 검진성공, 충치}) = P(\textrm{치통 | 충치})$$
$$P(\textrm{치통, 검진성공 | 충치}) = P(\textrm{치통 | 충치})P(\textrm{검진성공 | 충치}) \rightarrow P(X, Y |Z) = P(X|Z)P(Y|Z)$$
바로 세 번째 식은 조금 생소한데, 이에 대한 아래 증명을 참고하자.

즉, 두 변수가 marginally independent 하지 않더라도, 3번째 변수를 관측한 결과로써, 두 변수가 독립이 될 수 있다.
정의는 다음과 같다.
랜덤 변수 X 는 랜덤 변수 Z 가 주어졌을 때, Y에 대하여 conditionaly independent 하다.
$$\textrm{if, for all } x_i \in domain(X), y_k \in domain(Y), z_m \in domain(Z) \,\, P(X = x_i, Y = y_k, Z = z_m) = P(X=x_i, Z = z_m)$$
즉, Z 에 대한 정보가 주어졌을 때, Y의 값은 X 에 대한 믿음에 영향을 주지 못한다.
conditional independence 를 사용하면 joint distribution 의 표현 크기를 획기적으로 줄여준다. (exponential n $\rightarrow$ linear n )
$P(치통 | 검진성공, 충치) P(검진성공 | 충치) P(충치)$
marginally indepedent 하면 모두 독립이므로
$P(치통) \times P(검진성공) \times P(충치)$
conditionally independent 하면
$P(치통| 충치) \times P(검진성공 | 충치) \times P(충치)$
참고글
https://www.cs.ubc.ca/~carenini/TEACHING/CPSC322-10/SLIDES/lecture26-2010.pdf
Navie Bayes classifier

$f^* = argmax_{Y=y} P(X=x|Y=y)P(Y=y)$
기존 joint 과정에서 필요하던 parameter의 개수가 $2^d -1$ 였다.
여기에 모든 $x_1 ... x_6$ 에 conditional indepdent assumption 을 적용해보자.
$P(Y=y)$ prior 파트는 변함이 없다.
하지만 $P(X=x|Y=y)$ 해당 파트는 아래와 같이 곱샘으로 변하게 된다.
$\prod_{1 \leq i \leq d} P(X_i = x_i | Y = y)$
$$f^* \approx argmax_{Y=y}P(Y=y)\, \prod_{1 \leq i \leq d} P(X_i = x_i | Y = y)$$
개수는 $(2-1)dk = dk$ 개로 줄어들게 된다. (d: feature 개수 k: prior 개수(answer))
conditional independent assumption 은 당연히 틀리다. 그럼에도 너무 많은 파라미터 학습을 피하기 위한 어쩔 수 없는 선택이다.
가정 자체가 너무 약하다보니 Naive Bayes Classifier 라 명칭하였다.
Given:
Class Prior P(Y)
d conditionally independent features X given the class Y
For each $X_p$ we have the likelihood of $P(X_i | Y)$
Naive Bayes Classifier Function
$f_{NB}(x) = argmax_{Y=y} P(Y=y) \, \prod_{1 \leq i \leq d} P(X_i = x_i | Y = y)$
Naive Bayes Classifier 도 output의 bayes risk를 줄이려고 한다는점에서 optimal classifier 긴 하다.
Navie Bayes Problems
1. Naive 가정
현실에서 통용되지 않는 가정이다.
2. 부정확한 확률 측정
관측못한 sparse 한 Input 케이스가 있는 경우에 관측을 못한다. navie bayes classifier 가 이때는 동작하지 못한다. 이로 인해 MLE 보다는 MAP 를 사용해서 개별 확률 값을 만들어줘야 한다.
MLE 는 관측되지 않은 내용에 대해 estimation이 제대로 안된다. 이로 인해 MAP 를 통해 사전 정보라도 줘서 계산을 해야한다.
한번도 관측되지 않은 상태에 대하여 MLE 로 예측하면 확률값이 0 이 된다.
Application
Naive Bayes Classifier 의 실제 적용 사례를 살펴보며 익숙해지자.
예시는 아래에서 참고하였다.
https://www.datacamp.com/tutorial/naive-bayes-scikit-learn
Naive Bayes Classifier Tutorial: with Python Scikit-learn
Sklearn Naive Bayes Classifier Python. Learn how to build & evaluate a Gaussian Naive Bayes Classifier using Python's Scikit-learn package.
www.datacamp.com
1. feature가 한개인 경우

날씨에 따라 나가 놀지 여부를 결정하는 데이터이다.
날씨가 Overcast 인 날, 나가노는지 여부를 알고싶다.
이에 따른 공식은 아래와 같다.
사전 정보를 활용한 MAP 기법으로 계산을 해보자.
여기서 사용된 사전 정보란, 평상시에 얼마나 자주 나가 노는지에 대한 여부 정도가 될 수 있다.
날씨가 Overcast 인 날, 나가 놀 확률
P(Yes | Overcast) = P(Overcast | Yes) P(Yes) / P (Overcast)
1. Prior 확률 구하기:
P(Overcast) = 4/14 = 0.29
P(Yes)= 9/14 = 0.64
2. Posterior 확률 구하기:
P(Overcast |Yes) = 4/9 = 0.44
나가 논 날 줄, 날씨가 overcast 일 확률
3. 계산하기:
P (Yes | Overcast) = 0.44 * 0.64 / 0.29 = 0.98(Higher)
즉, 날씨가 overcast 한 경우, 나가 놀 확률은 0.98 로 예측된다.
날씨가 Overcast 인 날, 나가 놀지 않을 확률
P(No | Overcast) = P(Overcast | No) P(No) / P (Overcast)
1. Prior 확률 구하기:
P(Overcast) = 4/14 = 0.29
P(No)= 5/14 = 0.36
2. Posterior 확률 구하기:
P(Overcast |No) = 0/9 = 0
나가 놀지 않은 날 중, 날씨가 Overcast 일 확률
3. 계산하기
P (No | Overcast) = 0 * 0.36 / 0.29 = 0
즉, 날씨가 overcadt 하지 않은 경우, 나가 놀 확률은 0 으로 예측된다.
이에 따라 나가 놀 확률이 훨씬 높다고 결정할 수 있다.
2. feature가 여러개인 경우

feature가 여러개인 경우 진가를 발휘한다.
날씨가 Overcast 하고, 온도가 Mild 한 날 나가놀지 아닐지를 분류해보자.
베이즈 공식에 따라 작성해보면 아래와 같다.
날씨가 Overcast 하고 온도가 Mild 할 때 나가 놀 확률
P(Play= Yes | Weather=Overcast, Temp=Mild) = P(Weather=Overcast, Temp=Mild | Play= Yes)P(Play=Yes)
1. Prior 확률 구하기:
P(Yes)= 9/14 = 0.64
2. Posterior 확률 요소 구하기:
P(Overcast |Yes) = 4/9 = 0.44 P(Mild |Yes) = 4/9 = 0.44
3. Posterior 확률을 계산하기:
P(Weather=Overcast, Temp=Mild | Play= Yes) = 0.44 * 0.44 = 0.1936(Higher)
4. 계산하기:
P(Play= Yes | Weather=Overcast, Temp=Mild) = 0.1936*0.64 = 0.124
날씨가 Overcast 하고 온도가 Mild 할 때 나가 놀지 않을 확률
P(Play= No | Weather=Overcast, Temp=Mild) = P(Weather=Overcast, Temp=Mild | Play= No)P(Play=No)
1. Prior 확률 구하기:
P(No)= 5/14 = 0.36
2. Posterior 확률 요소 구하기:
P(Weather=Overcast |Play=No) = 0/9 = 0 P(Temp=Mild | Play=No)=2/5=0.4
3. Posterior 확률을 계산하기:
P(Weather=Overcast, Temp=Mild | Play= No) = 0 * 0.4= 0
4. 계산하기:
P(Play= No | Weather=Overcast, Temp=Mild) = 0*0.36=0
확률 비교를 통해 Overcast 날씨와 Mild 온도에 나가노는 것으로 확인되었다.
feature가 1 개일 때는 분모가 존재했는데 feature가 여러개가 되고, conditional independence를 가정하자 갑자기 분모가 사라졌다.
위 내용을 recall 해 보면,
$f^* = argmin_f P(f(X) \neq Y)$
$f^* = argmax_{Y-y} P(Y = y | X = x)$
Bayes Theorem 에 의해 아래와 같이 정리했다.
$= argmax_{Y=y} P(X = x | Y = y) P(Y = y)$
사실 조건부 확률에 따르면 아래 인것이 자명하다.
$P(Y | X) = \frac{P(X|Y) P(Y)} {P(X)}$
그럼 왜 분모를 생략하게 되었을까?
오랜 고민끝 아래의 결과에 이르렀다.
argmax_{Y=y} 에서 분모는 상수이다.
상수를 생략해도 Y가 나올 확률을 최대화 하는 상황은 같으므로 생략한 것으로 보인다.
아래는 위키백과를 참고하였다.

-
베이즈 정리의 분모에 해당하는 부분은 가능도를 구할 때 조건으로 걸린 사건(위의 예의 경우, (실제 병의 유무와는 상관 없이) '양성 판정이 나올 확률')의 확률이다. 기능적으로는 사후 확률이 확률의 정의(0 이상 1 이하여야 한다)를 충족시키도록 사전확률과 가능도의 곱을 보정해주는 역할을 한다. 위와 같은 예에서는 쉽게 계산할 수 있고 엄밀하게 사후확률을 구하려면 반드시 필요한 부분이지만, 실제로 생각보다 계산이 까다로울 경우 등식을 비례 관계로 바꾸고 생략할 수도 있다.
즉, 분류에 있어서 분모는 중요하지 않다. 그리고 애초에 conditional indenpendence 가정 자체가 확률을 구할 때 정확하지 않지 않은가?
'AI > 머신러닝' 카테고리의 다른 글
| 머신러닝 정리 7 - Decision Boundary, logistic regression, Gradient Descent (2) | 2022.10.28 |
|---|---|
| 머신 러닝 정리 7.5 - Gradient Descent 가 정말 잘 동작할까? (0) | 2022.10.28 |
| 머신 러닝 정리 5 - Linear Regression (0) | 2022.10.06 |
| 머신 러닝 정리 4- Decision Tree (1) | 2022.10.05 |
| 머신 러닝 정리 3 - 룰 베이스 알고리즘이란? (0) | 2022.09.29 |




