베이즈 아주 얕은 정리

베이즈를 활용해서 연구도 해봤고, 어느정도 이해했다고는 생각하지만 항상 약간만 깊이 들어가면 내가 아무것도 모르는 구나를 깨닫게 된다. 

 

이론적으로 완벽할 필요는 없지만 어느정도 구조에 대한 파악이 필요하다고 생각한다. 

 

아래 블로그는 웹서핑 과정 중에서 만난 여지껏 어떤 블로그보다 베이즈에 대한 개괄을 잘 작성해놓은 블로그이다. 

 

본 글은 내 사전지식에 맞춰 좀 덜거나 더해 작성되었기에 해당 글을 읽는 것보다 아래의 블로그 글을 읽는 것이 더 좋을 것 같다. 물론 나랑 사전 지식이 비슷하다면 이 글이 오히려 좋을 수도 있다. 

 

http://posterior.egloos.com/9606941

베이즈 정리 (일반적 형태)

 

대부분 글의 표현과 이미지는 위 블로그에서 가져온 것임을 먼저 밝힌다. 

 

 

베이지안 추론 

베이지안 추론은 '주관적 확률'을 사용할 수 있다는 점에서 전통적 절차와 큰 차이점을 지닌다. 

 

※주관적 확률이란 어떤 사건의 발생 또는 어떤 명제가 참임에 대한 믿음의 정도 (degree of belief) 를 0 에서 1 사이의 숫자로 나타낸 것이다. 이를테면 동전을 하나 던졌을 때 앞면이 나올 확률이 0.5라고 말하는 것은 '앞면과 뒷면이 나올 가능성은 동일하다' 라는 믿음을 반영하는 것이다. 

 

배경 지식을 반영할 수 있다는 엄청난 이점과, 이를 통해 여러 '주관적 확률 가설' 중 어느것이 더 확률적으로 그럴듯한지 비교해볼 수 있다. 

 

대표적인 예시로 장마철 기상청은 장마 시기의 비올 확률이라는 사전 지식을 예측에 활용한다. 

최근 예측 결과가 좀 좋지 않은데 여러 가설을 이용해보거나, 아예 사전 지식을 빼보면 어떨까? 

 

 

베이즈 정리

모든 베이지안 통계분석 절차는 베이즈 정리의 특수한 적용 사례에 불과하다. 베이즈정리의 토대가 되는 개념인 조건부확률을 살펴보자. 

 

※조건부확률이란 어떤 사건(명제)이'참'일 때 다른 사건(명제)이 참일 확률을 의미한다. 

 

'동전이 공평함' 이라는 전제 하에 동전이 앞면이 나올 확률이 0.5

 

P('앞면' | '공평한 동전') = 0.5

 

'동전이 심하게 굽음' 전제 하에 앞면이 나올 확률이 0.8

 

P('앞면' | '굽은 동전') = 0.8

 

조건부확률의 개념을 토대로, 베이즈정리는 다음과 같은 공식으로 표현된다.

 

$$P(A|B) = \frac{ P(B|A) \times P(A) }{ P(B) }$$

 

$P(A|B)$ : 사후 확률

$P(A)$ :  B가 참임을 알기 전에 A에 대해 갖고 있던 믿음(확률)을 의미, 사전확률

$P(B|A)$ : 우도, Likelihood 

$P(B)$ : 증거, evidence

 

예시) 동전은 공평한가?

 

가설이 두개밖에 없다고 가정하자. 

 

• 만약 동전이 공평하다면, 그것이 앞면이 나올 확률은 0.5이다.
• 만약 동전이 공평하지 않다면, 그것이 앞면이 나올 확률은 0.4이다.

 

2번의 시행에서 뒷면, 뒷면의 결과를 얻었다. 

 

이 동전이 공평할 확률은? 

 

$P(A|B)$ : 사후 확률

$P(A)$ :  0.5 

$P(B|A)$ : 0.5 X 0.5 = 0.25 

$P(B)$ : 0.5 X 0.25 + 0.5 X 0.36

 

분모의 계산은 분자보다 다소 까다롭다. P(B)가 의미하는 것은 'B가 일어날 확률' 인데, 이것을 조금 확장하여 생각하면 모든 가능한 상황에서 B가 일어날(참일) 확률의 합 이라 볼 수 있다. 그런데 위 경우에서 모든 가능한 상황이란 단 두 가지, 즉 동전이 앞면이 나올 확률이 0.5이거나 0.6인 경우로 제한되었다. 따라서 각각의 상황에서 뒷면이 두 번 나올 확률을 계산하여 더해야 한다. 하지만 여기서 주의할 것은 확률을 그냥 더하면 되는 것이 아니고, 각각의 우도에 사전확률을 가중치로 곱하여 더해야 한다. 이것은 각각의 가능성에 대한 사전믿음을 반영하는 것이다. 

 

$$P(A|B) = \frac{ P(B|A) \times P(A) }{ P(B) } = \frac{0.5 \times 0.25}{ 0.5 \times 0.25 + 0.5 \times 0.36} \approx 0.41 $$

 

동전이 공평하다는 가능성인 사후확률이 0.41 임을 확인하였다. 상단에서 제시하였지만 사후확률은 여러 가설 중 어떤 가설이 얼마나 현상을 잘 설명하는 가에 대한 지표이다. 

 

앞면이 나올 사전 믿음이 0.4인 경우 

 

$$P(A|B) = \frac{ P(B|A) \times P(A) }{ P(B) } = \frac{0.4 \times 0.36}{ 0.4 \times 0.25 + 0.4 \times 0.36} \approx 0.59 $$

 

앞면이 나올 확률이 0.4 라고 믿는 경우가 0.5 라고 믿는 경우보다 뒷면이 2번 연속 나온 것을 (0.59 - 0.41) 만큼 더 잘 설명한다. 

 

위 예시는 동전이 앞면이 나올 확률은 0.5이거나 0.6인 경우밖에 없으며, 그 외의 값은 갖지 않는다고 간주했다. 

그러나 실제로 베이지안 데이터분석을 할 때는 가설이 이와 같이 뚝뚝 떨어진 (이산적인) 경우는 흔치 않다. 이를테면 동전이 앞면이 나올 확률은 0에서 1 사이의 어느 값이나 가능다고 가정한다. 이런 경우에는 앞에서 설명한 방식으로 베이즈 정리를 사용하는 것은 불가능하다. 따라서 이번 글에서는 그러한 경우에도 일반적으로 사용할 수 있는 베이즈 정리의 형태를 알아보자. 

 

베이즈 정리의 일반적 형태

 

$$P(H|D) = \frac{P(H) P(D|H)} {P(D)}$$

 

통계분석 장면에서 가설은 모수치에 대한 어떤 명제를 의미한다. 더 쉽게 말하자면, 통계적 가설은 다음과 같은 형태를 갖는다: '신약의 치료효과는 0과 같다.' '동전이 앞면이 나올 확률은 0.5보다 크다.' 여기서 '신약의 치료효과', '동전이 앞면이 나올 확률' 등은 모수치에 관한 진술로 바꿀 수 있다. 전자의 경우에는 '신약의 치료효과' 를 θ로 나타내기로 하면 가설을 'θ=0' 과 같이 나타낼 수 있다. 후자의 경우에도 비슷하게 'p > 0.5' 와 같이 나타낼 수 있다. 다시 말해, 가설(H)은 모수치(θ)에 관한 진술이다. 따라서 위의 베이즈 정리를 아래와 같이 나타낼 수 있다.

 

$$P(\theta|D) = \frac{P(\theta) P(D|\theta)} {P(D)}$$

 

 

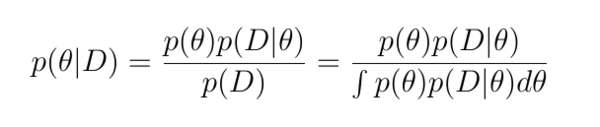
위 공식의 분모 P(D) 는 추론 과정에서 중요한 역할을 하지 않는 경우가 많는데, 상수로 취급되기 때문이다. (아마도 적분해서 1) 경우에 따라서는 중요하기도 하다. 

 

P(θ|D)는 사후확률(posterior), P(θ)는 사전확률(prior), P(D|θ)는 우도(likelihood) 임을 언급했다. 따라서 분모를 비례상수로 취급하면, 다음과 같은 표현을 얻게 된다:

 

정규분포 베이지안 업데이팅

베이지안에서 가장 흔하고, 가장 간단한 형태인 정규- 정규 모형을 살펴보자. 

이 글에서는 모분산을 이미 알고 있다고 가정하고, 단 하나의 자료를 관측했을 때 모평균에 대한 베이지안 추론을 한다. 

 

평균이 θ, 분산이 σ의 제곱인 정규분포 확률밀도함수는 아래와 같다. 

간단하게 수식을 통해 증명 과정을 살펴봤으나 생각보다 깨닫게 되는 점은 적다. 

 

이는 우도 (likelihood)에 해당된다. (우도는 P(D|θ)로 표현되었음을 상기하자.) 다시 말해 우도는 모수치가 주어졌을 때 자료(x)의 확률을 계산하는 데 사용되는 함수이다. (MLE 가 주어진 자료를 가장 잘 관찰할 수 있는 likelihood 를 말한다는 것을 떠올려보라!)

그런데 여기서는 분산이 상수라고 가정했기 때문에, 좌변에서 시그마(σ)를 생략해도 무방하다. 따라서 다음과 같이 다시 나타낼 수 있다.

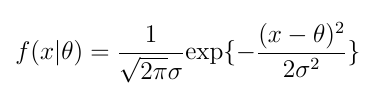
사후확률(사후분포) 을 계산하기 위해서는 사전확률도 필요하다. 사전 확률은 분석가가 사전에 할당하는 내용이다. 우도가 정규분포일 때 흔히 사용되는 정규사전분포(normal prior)를 사용한다.

위 식은 모평균(θ)에 대한 사전믿음을 평균이 m, 표준편차가 s인 정규분포로 표현한다. 좀 더 쉽게 말하자면, 위 사전분포를 사용하는 사람은 모평균이 대략 m이라 믿으며, 그 불확실성이 대략 s만큼이라고 믿는다는 것을 의미한다. 분석가가 s에 작은 값을 할당한다면 그것은 모평균이 m이라는 것에 대해 확신이 있다는 것을 의미하는 것이다. 반대로 큰 s의 값은 모평균이 m이라는 믿음에 대해 확신이 그만큼 없다는 것을 의미한다.

 

위와 같이 정규분포 우도함수에 정규사전분포를 함께 사용하는 통계모형을 정규-정규 모형(normal-normal model)이라 부른다.

 

아래의 식을 상기해보자. 

이 표현을 위에 적용하면 다음과 같은 결과를 얻게 된다. 편의상 사전분포와 우도의 순서를 바꾸었다. (x가 데이터, D에 해당된다.)

 

위 식을 θ에 대한 함수(확률밀도함수)로 보고, 이런저런 복잡한 계산과정을 거치면 다음과 같이 정리가 된다. (구체적인 계산 과정은 생략한다. )

 

 

수식이 매우 복잡하게 보인다. 하지만 개념적으로만 접근해 보자. 위 식 자체도 사실 정규분포의 공식처럼 보인다. 좀 더 구체적으로는, 위 식은 x가 주어졌을 때 θ 가 정규분포를 따른다는 것을 의미하는데, 이는 모평균에 대한 사후믿음이 정규분포임을 의미한다. (이는 사전분포로 정규분포를 사용한 결과다.) 

 

(정규분포 확률밀도함수랑 비교했을 때 $\sqrt{2\pi}$ 가 생략되었으나 아래 글에 따르면 이는 normalizing constant 라 한다.)

https://math.stackexchange.com/questions/3181774/what-is-the-purpose-of-frac1-sigma-sqrt2-pi-in-frac1-sigma-sqrt

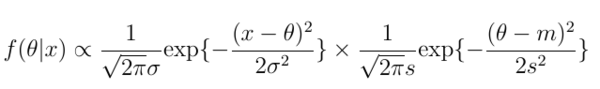
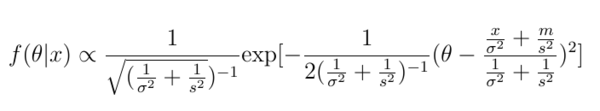
(정규분포 밀도함수 숨은 의미)

https://basicstatistics.tistory.com/entry/%EC%A0%95%EA%B7%9C%EB%B6%84%ED%8F%AC%EC%9D%98-%ED%99%95%EB%A5%A0%EB%B0%80%EB%8F%84%ED%95%A8%EC%88%98-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0

한편 정규분포 공식(밀도함수)의 형태를 참조하면, 위 식에서 사후분포의 평균과 분산은 다음과 같음을 알 수 있다

 

m' 은 사후분포의 평균, s' 은 사후분포의 분산을 나타낸다. 다시 말해, x라는 하나의 데이터를 관찰했을 때, 우리의 모평균(θ) 에 대한 믿음은 다시 정규분포로 기술될 수 있으며, 그 평균과 분산은 각각 m' 와 s' 가 된다.

 

사실 위 업데이트 과정은 베이지안 추론 일반에 적용되는 아주 중요한 의미를 담고 있다. 베이지안 추론은 사전믿음(사전분포)와 데이터에서 획득된 정보 사이의 타협이라는 것이다. 

 

 

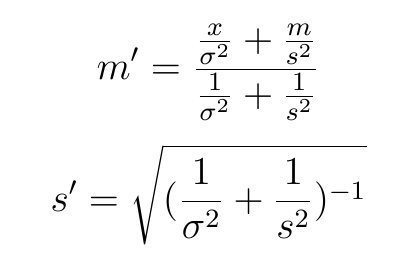
베이지안 업데이팅에 내포된 의미

Precision

 

 베이지안 통계학에서는 정규분포에 대해 이야기할 때, precision 이라는 개념을 분산 대신 사용할 때가 많다. 여기서는 이를 '정밀도' 와 비슷한 개념이라 생각하기로 하자. precision은 분산의 역수로 정의한다. 

 

통계학에서는 흔히 분산을 불확실성의 척도로 본다. 그런데 위 식을 보면 알 수 있지만, 분산이 커질수록 precision은 감소한다. 극단적인 경우, 분산이 무한대가 되면 precision은 0이 되고, 반대로 분산이 0에 가까워지면 precision은 무한대가 된다. 따라서 precision이 클수록 불확실성이 작다는 의미가 된다.

그런데 앞의 글에서 베이지안 업데이팅에 대해 이야기할 때, 모평균에 대한 분산의 업데이트 결과는 다음과 같다는 것을 확인했다.

사후분산(s' 의 제곱)의 역수는 사전분산(s의 제곱)의 역수에 자료 분산의 역수를 더한 것과 같다. 그런데 방금 precision은 분산의 역수라고 말했다. 따라서 앞의 진술을 다시 표현하면, 사후분포의 precision은 사전분포의 precision 과 자료의 precision의 합으로 나타낼 수 있다. (precision은 가법적 additive 이다.) 

 

 

이것의 함의는 무엇인가? 만약 자료의 precision에 비해 사전분포의 precision 이 매우 크다면, 자료의 precision(분산)은 사후분포의 precision에 별 영향을 끼치지 못할 것이다. 그런데 큰 precision은 사전분포에 대한 강한 믿음을 반영한다. 이는 강한 사전믿음일수록(사전분포가 강할수록) 자료에 의해 영향을 덜 받는다는 것을 의미한다. 반대로 사전분포에 대한 확신이 작다면 사전분포의 precision은 작아질 것이고, 따라서 사후 precision은 사전 precision보다는 자료의 precision에 더 큰 영향을 받게 된다. 이 사실은 향후에 사전분포를 만드는 방법에 대해 논의할 때 다시 등장하게 될 것이다.

 

이번에는 모평균에 대한 사후분포의 평균을 살펴보자. 정규-정규 모형에서 사후분포의 평균 (m') 은 다음과 같았다.

 

여기서 분자를 좀 더 자세히 들여다보자. 분자는 다음과 같이 다시 표현할 수 있다.

이것은 무엇을 의미하는가? 사후분포의 평균은 결국 자료(x)와 사전분포의 평균(m)에 의해 결정되는데, 각각에는 가중치가 곱해진다. 그런데 그 가중치들을 자세히 보면, 결국 앞서 이야기했던 precision 들이다. x와 m은 각각의 precision을 가중치로 받는 것이다. 또한 사전분포의 precision 이 클수록 사전평균(m)이 사후평균에 기여하는 정도가 커지고, 자료의 precision이 클수록 자료(x)가 사후평균에 기여하는 정도가 커진다. 따라서 이것은 사전분포나 자료에 대한 확신이 강할수록 그것이 사후적 판단에 끼치는 영향이 더 커야 한다는 우리의 직관을 잘 반영한다.

 

한 가지 더 확인할 수 있는 것은 이 글 서두에서 말한, 베이지안 업데이팅은 자료와 사전믿음 사이의 타협이라는 것이다. 위 식이 의미하는 것은, 결국 사후믿음(분포)은 자료와 사전믿음의 가중된 합이라는 것이다. 극단적인 경우, 자료의 precision이 0인 경우에는 사후평균은 전적으로 사전평균에 의해 결정된다. 반대로 사전분포의 precision이 0인 경우에는 사후평균은 자료에 의해 전적으로 결정된다. 그러나 두 precision이 모두 0이 아니라면, 사후평균은 x와 m 사이의 어떤 값이 될 것이다. 이는 베이지안 업데이팅이 자료와 사전믿음 사이의 타협이라는 결과를 낳음을 보여 준다.

이 결과는 앞으로도 반복하여 등장할, 베이지안 통계에 내재되어 있는 일종의 '철학' 이라고 간주해도 좋다.

 

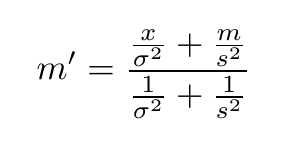
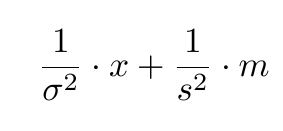
여러 자료로 구성된 표본을 갖고 있는 경우에 대해 예를 들어보자. (이 자료들은 공통의 정규분포에 왔으며, 각각은 독립이라고 가정한다.)

언제나 그렇듯, 베이지안 통계분석의 출발은 아래의 표현이다:

예시를 위해 정규분포에서 온 크기가 5인 표본 (5.1, 4.8, 4.9, 5.5, 5.3) 이 있다고 하자. 그리고 모분산은 0.1로 알려져 있다고 가정하자. 이 상황에서 정규-정규 모형을 이용하여 모평균에 대해 베이지안 업데이팅을 하려고 한다.

 

일단 사전분포를 설정해야 하는데, 사전분포의 평균이 4라고 가정하자. 그리고 사전분포의 자의성이 분석에 미치는 영향을 최소화하기 위해 precision 을 아주 작게 잡도록 하자. 이를테면 여기서는 0.001 로 잡겠다. 이는 모평균이 4라는 믿음에 대한 확신이 비교적 작음을 의미한다. (앞으로도 이와 같이 약한 사전분포를 사용하는 것을 자주 볼 것이다.)

 

이제 모평균 θ 에 대한 사전믿음(분포)을 다음과 같이 나타낼 수 있다.

 

이제는 우도를 결정해야 한다. 그런데 정규분포에서 온 자료가 있을 때, 이 자료가 모평균에 대해 주는 정보는 표본평균(sample mean)에 모두 들어 있다. 이와 같이 어떤 표본이 있을 때, 표본이 모수치에 대해 제공하는 모든 정보를 담고 있는 통계량을 충분통계량(sufficient statistic) 이라 부르며, 베이지안 통계에서 중요한 위치를 차지한다. 대개 어떤 자료가 있을 때, 그것을 이용하여 모수치에 대한 추론을 할 때는 전체 자료 대신 충분통계량만 사용하면 되는 경우가 많다. 충분통계량에 대한 자세한 수학적 묘사는 생략한다. 

 

한편 앞서의 글들에서 베이지안 업데이팅의 결과는 다음과 같다고 언급했었다.

 

 

이제 이 공식을 이용하여 베이지안 업데이팅을 해 보자. (위 공식에서 x 대신 표본평균이 들어갈 것이다.) 사후분산 (s') 은 이미 알려진 숫자들을 이용하여 쉽게 구할 수 있다. 자료의 분산은 0.1로 이미 알려져 있다고 가정했으므로 크기가 5인 자료의 표본평균의 분산은 이것을 자료 크기로 나눈 0.02가 된다. 따라서 자료의 precision은 1/0.02=50 이 된다. 한편 사전분포의 precision은 0.001로 가정했다. 따라서 사후 precision은 50+0.001 = 50.001 이 된다. 수학적 표현은 다음과 같다.

 

이제 m' 을 업데이트해 보자. 자료가 여러 개 있을 때, 이 값의 분자에는 다소의 수정이 가해진다. x가 더이상 하나의 숫자가 아닌 표본평균(충분통계량) 이 되고, 그 precision도 재조정되어 표본평균의 분산의 역수가 된다. 따라서 다음과 같은 형태가 된다.

한편 자료의 평균은 5.12 이다. 이제 사후평균을 구하기 위한 준비는 모두 끝났다. 한 가지 팁이라면, 사후평균의 분모는 사후 precision 과 같다는 것이다. 이제 숫자들을 대입해 보자.

 

사전분포에 대한 믿음을 아주 약하게 주었기 때문에, 사후평균은 표본평균에 아주 가까운 것을 확인할 수 있다. 이제 사후분포를 확정해 보자. 위에서 구한 사후평균과 사후 precision을 활용하면 된다.

 

그런데 만약 사전분포에 대한 믿음이 강했다면, 다시 말해 사전 precision이 컸다면 결과는 어땠을까? precision을 0.001에서 10으로 늘려 보도록 하자. 그러면 사후분포의 평균에 대한 베이지안 업데이팅 결과는 다음과 같이 바뀐다.

 

이전의 업데이팅 결과에 비해 사전평균 (4) 쪽으로 좀 더 옮겨간 것을 확인할 수 있다. 이 사례는 베이지안 통계절차가 사전믿음과 자료 사이의 타협이며, 양자에 대한 확신의 강도에 의해 사후 판단이 영향을 받을 수 있다는 것을 잘 보여준다.

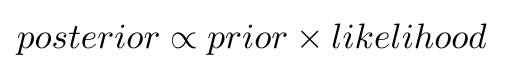
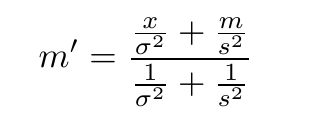
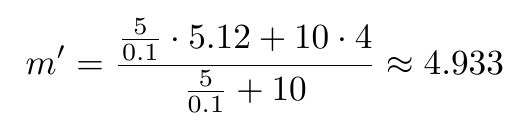
한가지 명확하게 하고 싶은 점은, 왜 표본 평균과 표본 평균의 분산을 사용했다는 점이다. 

 

위글을 읽고 아래의 글을 읽으면 정리하는데 도움이 된다. 

https://zzaebok.github.io/machine_learning/mle-bayes-mathematical-proof/

최대 우도 추정과 베이즈 정리의 간단한 수학적 증명

https://gaussian37.github.io/ml-concept-basic_bayesian_theory/

기초 베이지안 이론 (Basic Bayesian Theory)

https://github.com/markdregan/Bayesian-Modelling-in-Python

GitHub - markdregan/Bayesian-Modelling-in-Python: A python tutorial on bayesian modeling techniques (PyMC3)

켤레 사전 분포 

 

우도함수(데이터 생성모형)가 있을 때, 사전분포를 적절히 설정하면 사후분포가 사전분포와 같도록 만들 수 있다. 이러한 사전분포를 '켤레사전분포' (Conjugate prior distribution) 라 부르며, 베이지안 통계에서 흔히 사용한다. 켤레사전분포를 사용하면 사후분포가 우리가 잘 아는 분포가 되기 때문에 사후평균, 사후분산 등을 매우 쉽게 구할 수 있다.

 

켤레사전분포를 사용하는 이유는 계산이 편해지기 때문이다.  이를테면 정규-정규 모형에서 우도함수의 분산을 이미 안다고 가정하는 경우, 모평균의 기댓값에 대한 업데이팅은 다음과 같이 이루어짐을 이미 확인하였다:

 

이 과정에는 어떠한 프로그래밍이나 시뮬레이션도 필요하지 않으며, 단지 이미 아는 숫자들을 대입하기만 하면 된다. 사실 분산을 모른다고 가정하는 경우에도 분산에 대해 사전믿음을 켤레사전분포로 설정하면, 일련의 수학적 증명을 통해 분산이 어떻게 업데이트되는지 보일 수 있다. 이 과정에서도 단지 몇 가지의 간단한 숫자나 통계량(표본분산) 등을 대입하기만 하면 된다. (참고로 정규-정규 모형에서 분산에 대한 켤레사전분포로는 흔히 감마분포나 역감마분포, 역카이제곱분포라는 이름의 분포들을 즐겨 사용한다.)

 

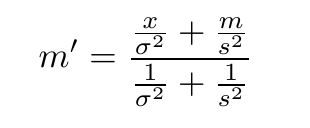
만약 사전분포가 켤레사전분포가 아니라면 수학적으로만 사후분포를 얻는 것은 매우 어려운데, 사후분포를 친숙한 분포의 형태로 구하는 것이 난해하기 때문이다. 따라서 사후분포로부터 평균이나 분산 등의 통계치를 얻기를 원하거나, 사후분포를 시각화하려는 경우에는 컴퓨터 시뮬레이션의 힘을 빌릴 수밖에 없다. 1990년대 이전에는 이것은 매우 어려웠다. 이론적으로도 힘들었거니와 당대의 컴퓨터의 성능이 이와 같은 복잡한 시뮬레이션을 수행하기에는 부족했기 때문이다. 그러나 기술의 눈부신 발전과 이론적 발전에 힘입어, 최근 들어서는 사전분포가 켤레사전분포가 아닌 경우에도 비교적 짧은 시간 안에 사후분포에 대한 시뮬레이션 결과를 얻을 수 있게 되었다. 이는 베이지안 통계학이 주류로 들어올 수 있게 해 준 중요한 계기가 되었다.

 

하지만 최근에도 켤레사전분포의 사용은 계속되고 있는데, 이는 켤레사전분포를 사용이 시뮬레이션 방법의 사용을 줄일 수 있게 해 주며 따라서 각종 시간적, 계산적 비용을 절감해줄 수 있기 때문이다.