꺼내먹는지식 준
그래프 이론 - Union, 크루스칼 알고리즘, 위상 정렬 본문
그간 몇가지 기본 알고리즘을 살펴보았다.
마지막으로 다양한 그래프 알고리즘을 살펴보고자 한다.
먼저 다룬 DFS/BFS, 최단 경로 알고리즘도 그래프의 일종이다.
출제 비중은 비교적 낮은 편이다.
그래프와 트리의 차이
| 그래프 | 트리 | |
| 방향성 | 방향 그래프 혹은 무방향 그래프 | 방향 그래프 |
| 순환성 | 순환 및 비순환 | 비순환 |
| 루트 노드 존재 여부 | 루트 노드가 없음 | 루트 노드가 존재 |
| 노드간 관계성 | 부모와 자식 관계 없음 | 부모와 자식 관계 |
| 모델의 종류 | 네트워크 모델 | 계층 모델 |
서로소 집합(union-find 자료구조)
수학에서 서로소 집합이란 공통 원소가 없는 두 집합을 의미한다.
예를 들어 {1,2} 와 집합 {3,4} 는 서로소 관계이지만, {1,2}와 {2,3}은 서로소 관계가 아니다.
서로소 집합 자료구조는 몇몇 그래프 알고리즘에서 매우 중요하다.
※ 서로소 집합 자료구조 : 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조이다.
합집합과 찾기 연산
- union: 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
- find: 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산
서로소 집합 자료구조는 트리 자료구조를 이용하여 집합을 표현한다.
알고리즘
- 1) union(합집합) 연산을 확인하여, 서로 연결된 두 노드 A, B 를 확인한다.
- A와 B의 루트노드 A', B' 를 각각 찾는다.
- A'를 B'의 부모노드로 설정한다. (B' 가 A'를 가리키도록 한다.)
- 2) 모든 union(합집합) 연산을 처리할 때 까지 1번 과정을 반복한다.
실 구현 단에서 A' 와 B' 중에서 더 번호가 작은 원소가 부모 노드가 되도록 구현하는 경우가 많다.
아래의 예제를 살펴보자. 이미지 출처 (https://esoongan.tistory.com/78)
- union 1, 4
- union 2, 3
- union 2, 4
- union 5, 6

초기에는 자기 자신을 부모로 가지도록 설정
현재 원소의 개수가 6개 이므로 총 6개의 트리가 있는 것과 같다. 부모테이블은 말 그대로 부모의 정보만 담고 있다. 즉 실제 루트를 찾기 위해서는 재귀적으로 부모를 거슬러 올라가야 한다.

첫번째 union(1,4) 연산으로 합친다. 더 큰 번호인 4의 부모를 1로 설정한다.

두번째 union(2,3) 연산으로 합친다. 더 큰 번호인 3이 2를 가리킨다.

세번째 union(2,4) 연산으로 합친다. 4가 2를 가리키는데, 2가 가리키는 1을 가리키게 된다.

네번째 union(5,6) 연산으로 합친다. 6이 5를 가리킨다.

- union 연산을 효율적으로 수행하기 위해 '부모 테이블'을 항상 가지고 있어야 한다.
- 루트 노드를 즉시 확인 불가능하고, 거슬러 올라가며 확인해야 한다. (루트노드는 부모가 자기 자신이다.)
코드 구현
입력예시
6 4
1 4
2 3
2 4
5 6출력
각 원소가 속한 집합: 1 1 1 1 5 5
부모 테이블: 1 1 2 1 5 5
import sys
input = sys.stdin.readline
v, e = map(int, input().split())
parent = [i for i in range(1, v+1)]
parent.insert(0, 0)
def find_parent(node):
return node if parent[node] == node else find_parent(parent[node])
def union(parent, node1, node2):
tmp1 = find_parent(node1)
tmp2 = find_parent(node2)
if tmp1 < tmp2:
parent[tmp2] = tmp1
else:
parent[tmp1] = tmp2
for i in range(e):
p, c = map(int, input().split())
# 1, 4
union(parent, p, c)
print("각 원소가 속한 집합", end = ': ')
for i in range(1, v+1):
print(find_parent(i), end = ' ')
print("부모 테이블:", *parent[1:])※ 코드 효율 개선 (경로 압축)
해당 문제 find 함수의 핵심은 노드의 루트를 찾는 것이다.
애초에 모든 노드의 parent 를 루트도 설정하면 찾는 시간이 단축될 것이다.
def find_parent(node):
return node if parent[node] == node else find_parent(parent[node])
def find_parent(node):
if parent[node] != node:
parent[node] = find_parent(parent[node])
return parent[node]상단 코드를 아래와 같이 바꿔주면 된다.
서로소 집합을 이용한 사이클 판별

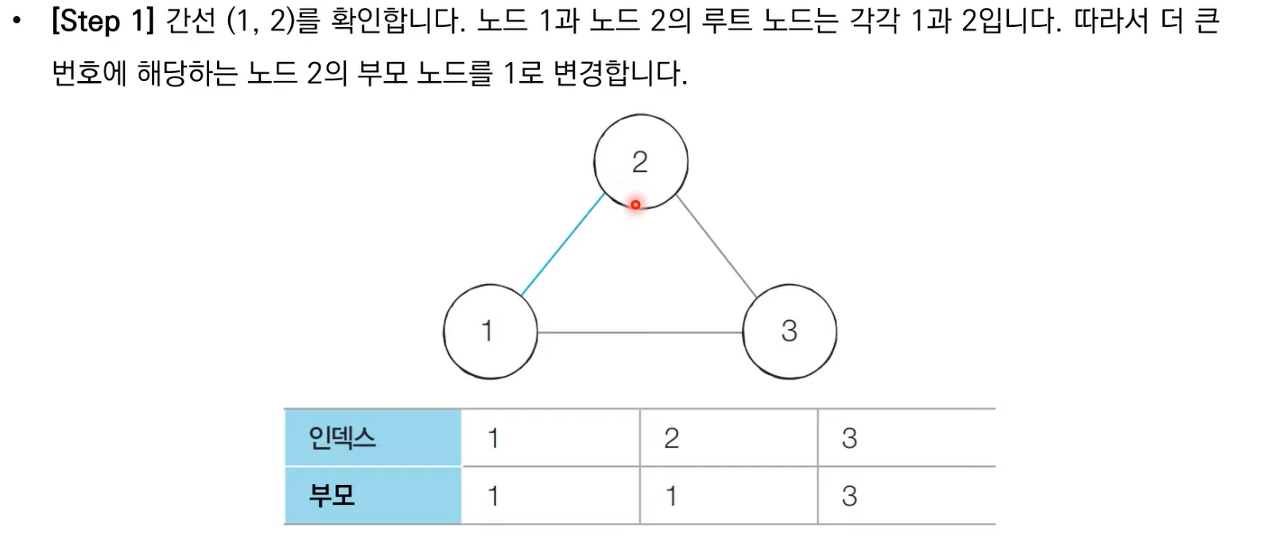

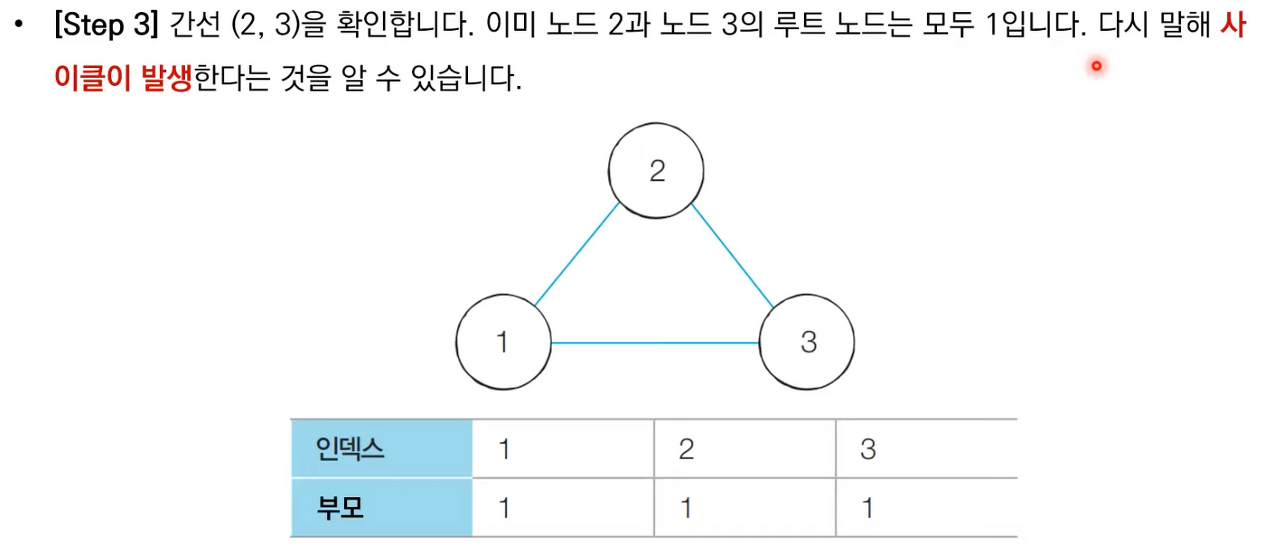
연결된 두개의 노드가 서로 다른 노드를 부모로 갖는 것은 사이클이 발생한 다는 걸 보여준다.
단, 해당 사이클 판별은 방향이 없는 무방향 그래프에서만 사용 가능하다.
코드 구현
import sys
input = sys.stdin.readline
n,e = map(int, input().split())
parent = [i for i in range(1,n+1)]
parent.insert(0,0)
def cycle_check(p1, p2, a, b):
if a < b:
if p1 != a and p2 != a:
return True
else:
if p1 != b and p2 != b:
return True
def union(parent, a, b):
p1 = find(parent, a)
p2 = find(parent, b)
if p1 == p2:
if cycle_check(p1, p2, a, b):
print("사이클이 발생했습니다.")
exit()
if p1 > p2:
parent[p1] = p2
else:
parent[p2] = p1
def find(parent,node):
if parent[node] != node:
parent[node] = find(parent, parent[node])
return parent[node]
for i in range(e):
a, b = map(int, input().split())
union(parent, a,b)
처음에는 사이클이 발생하는 과정을 좀 더 복잡하게 생각했다.
특정 노드 두개를 union 하는 과정에서 (1, 3) 노드가 각각 (1, 1)을 parent 로 갖는 경우를 고려하여 head 가 될 노드가 root 와 달라야만 cycle 이 발생했다고 report 하도록 처리했다.
하지만 다음의 해결책은 두가지 문제를 갖는다.
- 만약 (1,3) 노드가 각각 (1,1) parent 로 갖게 된 후, (2,3) 을 먼저 수행하게 되어도 각각 (1,1) parent 로 갖게된다. 그 후 (1,2) union을 수행하면 cycle 발생을 detect 해야 하는데 지금의 알고리즘은 해당 경우를 배제해버린다.
- (1,3) 의 parent 를 확인하면 초기 설정 전에는 (1,3) 으로 나타난다. 애초에 (1,1) 로 나타나지 않기 때문에 확인한 각각의 parent 가 (1,1) 이면 바로 사이클 발생임을 확인할 수 있다.
아래와 같이 코드를 수정한다.
import sys
input = sys.stdin.readline
n,e = map(int, input().split())
parent = [i for i in range(1,n+1)]
parent.insert(0,0)
def cycle_check(p1, p2, a, b):
if a < b:
if p1 != a and p2 != a:
return True
else:
if p1 != b and p2 != b:
return True
def union(parent, a, b):
p1 = find(parent, a)
p2 = find(parent, b)
if p1 == p2:
print("사이클이 발생했습니다.")
exit()
if p1 > p2:
parent[p1] = p2
else:
parent[p2] = p1
def find(parent,node):
if parent[node] != node:
parent[node] = find(parent, parent[node])
return parent[node]
for i in range(e):
a, b = map(int, input().split())
union(parent, a,b)크루스칼 알고리즘
union을 폭 넓게 이해하고 있으면 크루스칼 알고리즘은 정말 쉽게 이해할 수 있다. 정의는 아래에 기술된다.
신장 트리
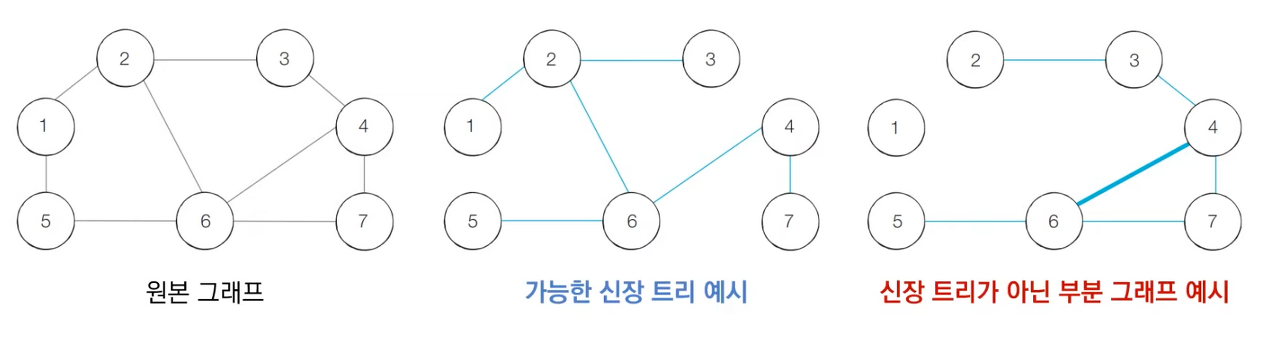
신장 트리는 모든 노드를 포함하면서 사이클이 존재하지 않는 그래프이다.
모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 성립 조건이기도 하다. 따라서 신장 트리라 한다.
다만 요지는 다음과 같다.
크루스칼 알고리즘: 주어진 그래프에서 최소한의 비용으로 신장 트리를 찾는 알고리즘

예를 들어 위 그림과 같은 그래프가 주어졌을 때, 모든 노드를 최소 비용으로 방문하는 것이 바로 최소 비용의 신장트리를 찾는 방법이고, 23, 13 이 이에 해당된다.
어떻게 하면 최소 비용으로 방문할 수 있을까?
간단하게 가장 작은 크기의 간선들을 포함시키면서, 사이클이 발생하는지 확인하여 사이클이 발생하면 포함 안하면 된다.
그러면 최소 비용으로 모든 노드를 방문할 수 있다.
이는 그리디 알고리즘의 특징이다. 크루스칼 알고리즘은 그리디 알고리즘이라고 할 수 있다.
동작 예시를 이미지로 보고 싶으면 아래 글을 참고하면 된다.
[2021 이코테] 8. 기타 그래프 이론
2021 이코테 강의 정리
velog.io
종료조건은 포함시킨 간선의 개수가 노드의 개수보다 1개 적은 순간이다.
(사이클 없이 노드들을 간선으로 연결하면 간선의 숫자가 노드보다 한개 적다. 이는 트리의 특징이기도 하다.)
코드 구현
우선 해당 구현을 위해 어떤 자료 구조가 필요한지 고민해보자.
1) 각 간선의 정보를 저장시킬 1D list
2) root 노드와 사이클을 확인 할 때 필요한 parent 1D list
구현 아이디어
간선이 들어오면 거리가 작은 순으로 정렬한다.
거리가 작은 순으로 union 을 수행한다.
cycle 이 발생하면 포함하지 않는다.
import sys
input = sys.stdin.readline
node, edge = map(int, input().split())
parent = [i for i in range(1, node+1)]
parent.insert(0,0)
lst = []
ans = []
for i in range(edge):
lst.append(list(map(int, input().split())))
lst.sort(key= lambda x: x[2])
def find_parent(parent, node):
if parent[node] != node:
parent[node] = find_parent(parent, parent[node])
return parent[node]
def union(parent, a, b):
p1 = find_parent(parent,a)
p2 = find_parent(parent,b)
if p1 == p2:
return False
if p1 > p2:
parent[p1] = p2
else:
parent[p2] = p1
return True
for s,e,d in lst:
if union(parent, s,e):
ans.append(d)
if len(ans) == (node-1):
print(sum(ans))
exit()
개수가 node-1 과 같아지면 이미 모든 간선이 포함된 것이므로 거기서 동작이 멈추면 된다.
물론 비교 횟수 자체가 오히려 연산 수를 증가시켰을 가능성이 있다.
애초에 union 의 사이클 확인 알고리즘 자체가 방향이 없는 무방향 그래프 즉 트리를 기반으로 한다.
그러므로 크루스칼 알고리즘도 무방향 그래프에서만 동작한다.
위상 정렬
순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘
즉, 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록' 순서대로 나열하는 것이다.
아무래도 사이클도 발생하지 않고, 동일한 노드로 들어가고 나가는 양방향성은 없다는 것이 직관적으로 판단된다.
대표적인 예시는 대학교 선수과목이다.
| 데이터 구조 | 알고리즘 | 고급 알고리즘 |
| 데이터 구조 | 알고리즘 | |
| 데이터 구조 |
데이터 구조는 선수과목이 없지만, 알고리즘은 데이터 구조를 수강해야 한다. 또한 고급 알고리즘은 알고리즘과 데이터 구조를 선수과목으로 수강해야 한다. 단, 순서는 데이터 구조 $\rightarrow$ 알고리즘 $\rightarrow$ 고급 알고리즘 순이다.
진입 차수
특정한 노드로 '들어오는' 간선의 개수
위 예시의 고급 알고리즘은 진입 차수가 '2' 이다.
위상 정렬 알고리즘
- 진입 차수가 0인 노드를 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
해당 내용 예시
워낙 간단한 개념이라 예시를 참고하지 않아도 풀 수 있을 것으로 보인다.
코드 구현
입력
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4출력
1 2 5 3 6 4 7import sys
input = sys.stdin.readline
from collections import deque
queue = deque()
node, edge = map(int, input().split())
graph = [[] for i in range(node+1)]
indegree = [0] * (node+1)
visited = [0] * (node+1)
for i in range(edge):
s, e = map(int, input().split())
graph[s].append(e)
indegree[e] += 1
for i,c in enumerate(indegree[1:]):
if c == 0:
queue.append(i+1)
while queue:
tmp = queue.popleft()
print(tmp, end = ' ')
if visited[tmp] == 1:
continue
visited[tmp] = 1
for node in graph[tmp]:
indegree[node] -= 1
if indegree[node] == 0:
queue.append(node)
실제 구현과 거의 동일하나, visited 을 따로 생성해줄 필요가 없다.
왜인고 하니, 양방향 그래프가 아니기 때문에 나간 간선이 다시 들어올 일이 없다.
실전 예제 2
마을은 N 개의 집과 집들을 연결하는 M 개의 길로 이루어져 있다. 각 길은 유지 비용이 다 다르다.
마을을 두개로 나누려고 한다.
각 분리된 마을에는 임의의 두 집 사이에 항상 경로가 존재해야 한다.(굉장히 헷갈리는 문구이다. 모든 노드들이 조합으로 각 두 노드당 간선 하나가 존재해야 하는 것은 아닌 것으로 보인다. 그냥 모든 노드가 포함 되면 되는 것 같다.) 마을에는 집이 하나 이상 있어야한다.
분리된 두 마을 사이에 있는 길들은 모두 없앨 수 있다.
길의 유지비를 최소로 하기 위한 프로그램을 작성하여라.
문제 해설
N개의 노드와 간선이 존재할 때, 두개의 신장 트리로 만들면서 최소 비용이 드는 경우를 찾으면 된다.
핵심은 어떻게 최소의 비용이 드는 두개의 신장트리를 만드느냐이다.
나눠진 마을은 노드간의 관계가 끊기므로, 유지비용이 큰 간선들을 끊어주는 것이 효율적이다.
아이디어는 신장 트리를 하나 만들고, 거기서 제일 큰 간선을 짤라 두개의 마을을 만드는 것이다.
import sys
input = sys.stdin.readline
v, e = map(int, input().split())
parent = [i for i in range(1, v+1)]
parent.insert(0,0)
lst = []
def find(parent, node):
if parent[node] != node:
parent[node] = find(parent, parent[node])
return parent[node]
def union(parent, a, b):
p1 = find(parent, a)
p2 = find(parent, b)
if p1 == p2:
return False
if p1 > p2:
parent[p1] = p2
else:
parent[p2] = p1
return True
for i in range(e):
lst.append(list(map(int, input().split())))
lst.sort(key = lambda x: x[2])
ans = []
for s,e,d in lst:
if union(parent,s,e):
ans.append(d)
if len(ans) == v-1:
print(sum(ans) - max(ans))
exit()실전 예제 3
각 수업은 선수 강의가 있다. 총 N 개의 강의를 들으려 한다. 동시에 여러 강의를 들을 수 있다고 가정한다.
N개의 수업을 모두 듣는다 할 때 각각 강의에 대해 수강을 위한 최소 시간을 출력하시오.
입력예시
5
10 -1
10 1 -1
4 1 -1
4 3 1 -1
3 3 -1총 수업 개수
수업시간, 선행 수강 수업, -1
출력
10
20
14
18
17그래프 관계

- 실수하기 좋은 점 1
5의 경우 3의 indegree 에 1을 더 더하여 indegree 가 2가 된다고 착오하였다.
이에 따라 4와 5는 아예 동일한 indegree 를 갖는다고 생각했는데, 실제로 두 indegree 값은 다르다.
- 실수하기 좋은 점 2
#time[num] = max(time[num], time[now]+time[num])
result[num] = max(result[num], result[now] + time[num])처음에는 최종 결과물과 각 노드의 시간이 적힌 테이블을 같이 사용해도 된다고 착오하였다.
하지만 이는 아래와 같은 문제를 발생시킨다.
step 1)
노드4를 업데이트 하기 위하여 노드 1의 값인 10 + 노드 4를 수강하는데 걸리는 시간 4 = 14

step 2)
노드4를 업데이트 하기 위하여 노드 1을 수강하고 노드 3을 수강한 시간 14 + 노드 4를 수강하는데 걸리는 시간(4) 14= 28
노드 4를 수강하는데 걸리는 시간은 4이지만 각 노드의 소요시간 테이블을 중복해서 쓴 결과 아래와 같이 저장이 되어버린 시간이 영향을 미쳐서 결과 값이 18이 아닌 28이 나오게 되었다.

특히나 두 번째 실수는 실수 사유를 아예 방향을 잘못 잡아 한참동안 고민을 해서 해결했다.
import sys
input = sys.stdin.readline
from collections import deque
import copy
N = int(input())
time = [0] * (N+1)
indegree = [0] * (N+1)
graph = [[] for i in range(N+1)]
queue = deque()
for i in range(1, N+1):
data = list(map(int,input().split()))
time[i] = data[0]
for num in data[1:-1]:
indegree[i] += 1
graph[num].append(i)
for i in range(1, N+1):
if indegree[i] == 0: queue.append(i)
result = copy.deepcopy(time)
while queue:
now = queue.popleft()
for num in graph[now]:
indegree[num] -= 1
if indegree[num] == 0:
queue.append(num)
#time[num] = max(time[num], time[now]+time[num])
result[num] = max(result[num], result[now] + time[num])
print(result[1:])
'코딩테스트총정리' 카테고리의 다른 글
| 그리디 기출 문제 05 볼링공 고르기 (0) | 2022.08.20 |
|---|---|
| 그리디 기출 문제 04 만들 수 없는 금액 (0) | 2022.08.19 |
| 최단 경로 - 플로이드 워셜 알고리즘 (0) | 2022.08.14 |
| 최단 경로 - 다익스트라 (0) | 2022.08.11 |
| 다이나믹 프로그래밍 (0) | 2022.08.10 |



