꺼내먹는지식 준
행 벡터의 의미와 내적 본문
모든 내용은 https://angeloyeo.github.io/2020/09/09/row_vector_and_inner_product.html
행벡터의 의미와 벡터의 내적 - 공돌이의 수학정리노트
angeloyeo.github.io
공돌이의 수학노트가 깨져보여서 더 잘 보기 위해 옮겨놓으며 원래 알던 부분들을 제외한 것 뿐입니다. 해당 포스트는 저를 위한 포스트이니 위 링크를 타고 들어가 나오는 강의를 따로 참고해주세요.
벡터란 상수배(곱셈 규칙)와 덧셈 규칙이 정의되는 원소들이라고 하였으며, 이들의 집합에 이 연산들이 정의된 집합을 벡터 공간(vector space)라고 한다고 하였다. 여기서 이러한 상수배와 덧셈
규칙이 정의되는 원소들을 ‘선형성을 갖는다’라고 표현한다.
행렬은 벡터를 또 다른 벡터로 변환 시키는 일종의 연산자로 볼 수 있으며, 특히 행렬과 벡터의 곱은 행렬의 열벡터들을 얼마나 선형결합 시킬 것인가라는 의미로 볼 수 있다.
해당 포스트에서는 행벡터의 기능과 역할, 그리고 벡터의 내적이 왜 기하학적으로 한 벡터에서 다른 벡터로의 정사영과 관련있는지 알아본다.

행벡터의 기능과 역할
열 벡터는 '변화의 대상'이 되는 것에 반해, 행 벡터는 변화를 시키는 '행위자'라고 해석할 수 있다.

행벡터의 시각화
입력 $x$에 대해 함수의 출력 $f(x)$를 대응시킨 좌표들을 나열한 것을 함수의 시각화라 한다.
그렇다면 $[2 \,\,\, 1]$ 이라는 행벡터를 시각화 한다고 하면, 임의의 벡터 $[x \,\,\, y]^T$ 에 대해 함수의 출력을 좌표계에 나열하면 된다.
$$ \begin{bmatrix} 2 & 1\end{bmatrix} \Big( \begin{bmatrix} x \\ y\end{bmatrix} \Big) = 2x + y = c$$
※ c는 스칼라
여러 스칼라 출력에 대한 함수를 하나의 xy 평면에 나타내보자.

이 개념은 등고선과 비슷하다.

높이가 같은 곳들을 곡선으로 이어 붙이면 어떤 부분이 더 가파른지에 대한 정보 파악이 가능하다.
이와 마찬가지로 scalar 값들에 대응하는 값들을 시각화할 수 있다.

$y = 2x-3$
...
$y = 2x +1$
$\Rightarrow \begin{bmatrix} 2 & 1 \end{bmatrix} \Big( \begin{bmatrix} x \\ y \end{bmatrix} \Big) = 1 $
...
$y = 2x +4$
여기서 이 순서쌍들 중 일부를 화살표 모양의 벡터 형태로 표시하면 아래의 그림 6에서 볼 수 있는 것들과 같다.
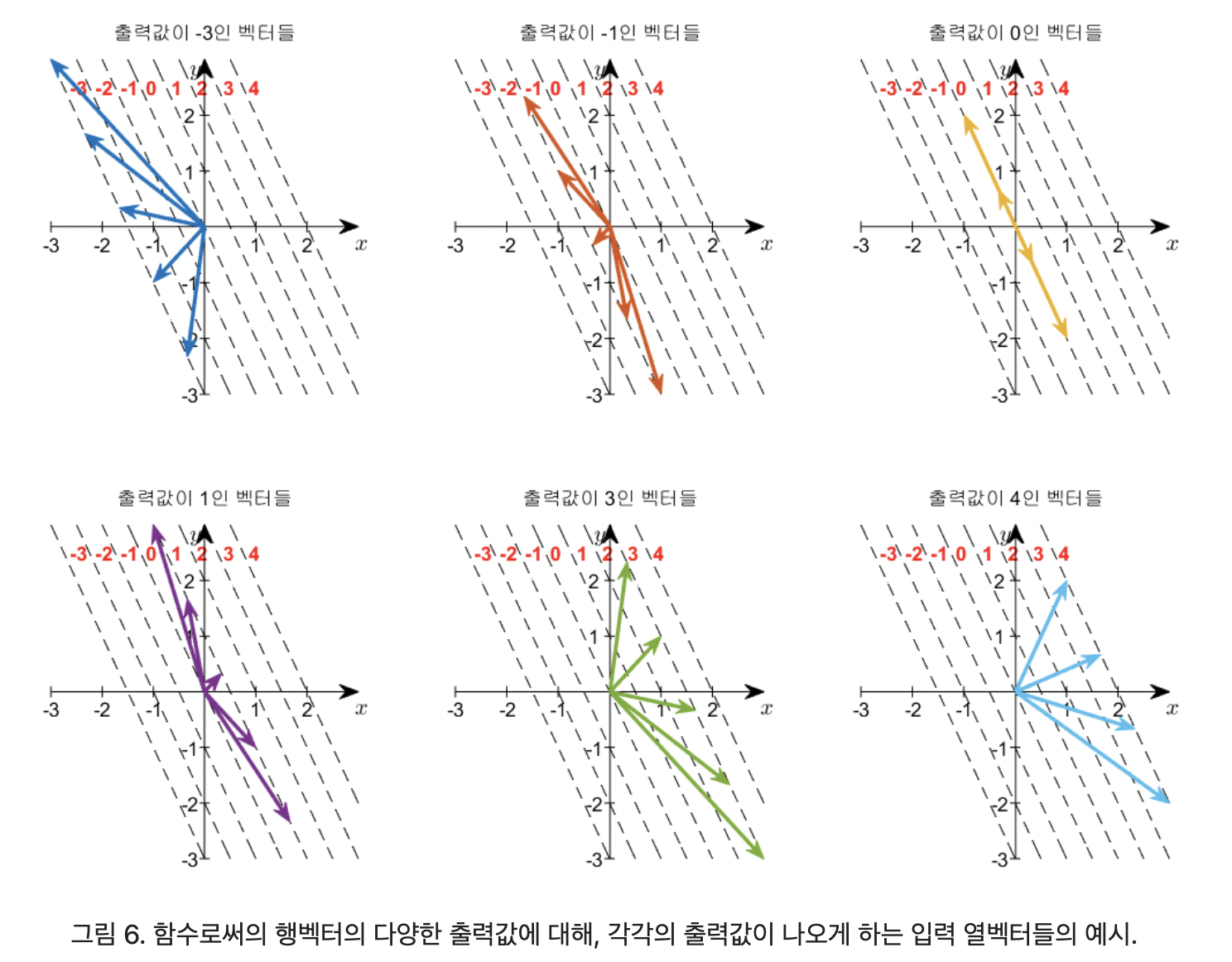
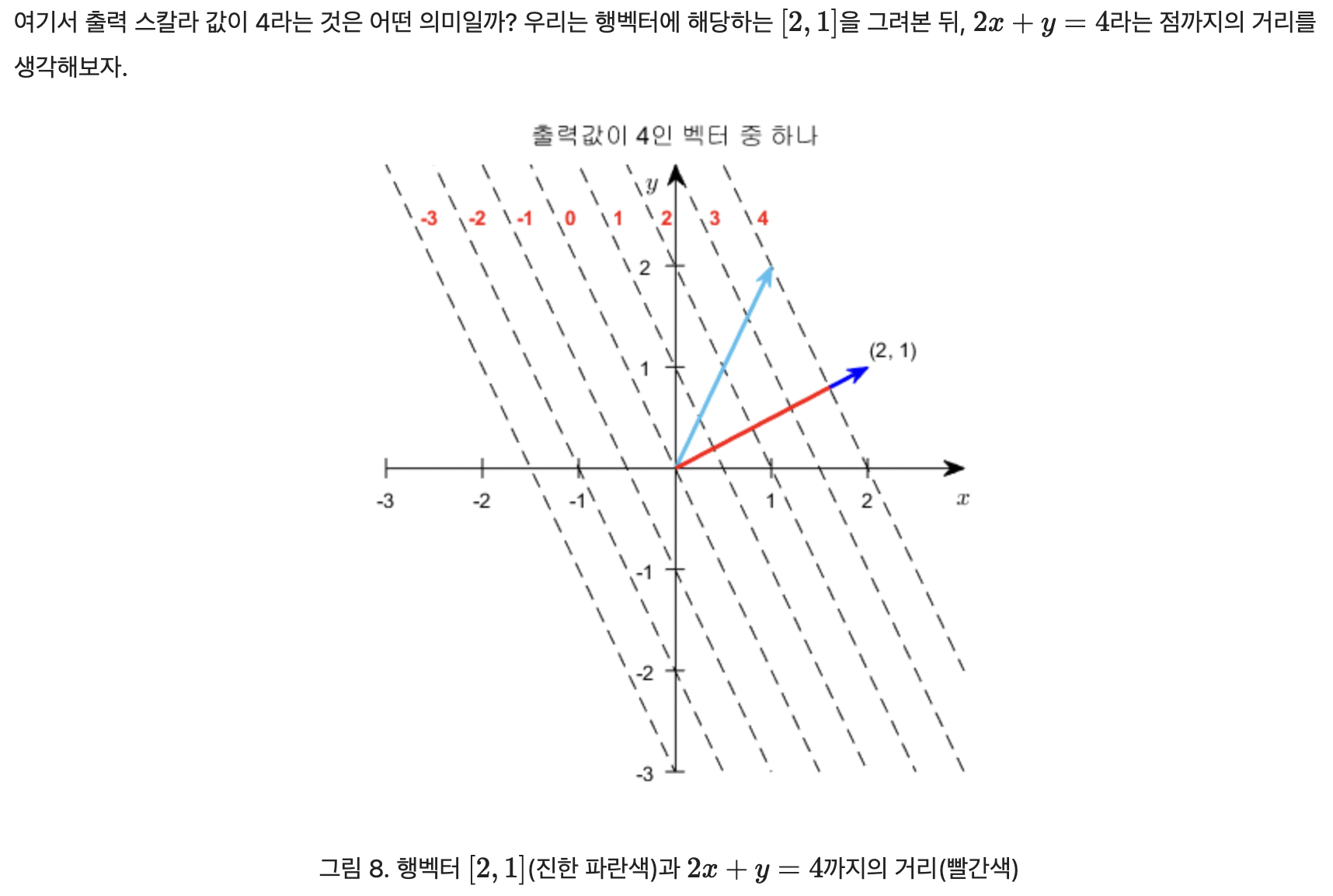
생각해보면 $에 해당하는 점선은 모두 행벡터 [2,1]에 수직이다. 왜냐면 행벡터가 점선으로 표현한 함수들에 대한 법선 벡터 역할을 하기 때문이다.



한번만 더 쉽게 정리하자면, '출력값이 4'인 벡터와 , 정사영 결과 '$|\vec{v_2}| cos\theta$' $\times$ '$|\vec{v_1}|$' 의 크기가 동일하므로 기하학적으로 확인이 완료되었다.
행벡터와 행공간
행벡터도 '열벡터'와 마찬가지로 벡터의 정의를 만족하며 선형성을 갖는다. (함수의 역할을 하는 것과는 상관 없이)


글이 컴팩트하고 모두 중요해서 버릴 부분이 하나도 없다. 이하 내용도 너무 중요하고 버릴 내용이 하나도 없다.
이해한 부분을 한마디로 정리해보자면 행 벡터는 결국 함수처럼 동작을 하고, scalar 값에 따른 함수를 좌표평면 위에 나타낼 수 있다.






해당 내용의 경우, 사실 선형 회귀 및 푸리에 변환을 하면서 다른 영역으로 전환하여 해결하는 경우들을 경험했는데 쌍대공간이라는 개념과 연관이 있는 건 처음 알았고 사실 아직 이해가 잘 안간다.

