꺼내먹는지식 준
CNN 간단 정리 본문
MLP는 각 뉴런들이 선형모델과 활성함수로 모두 연결된 구조였다.
Fully conneceted layer
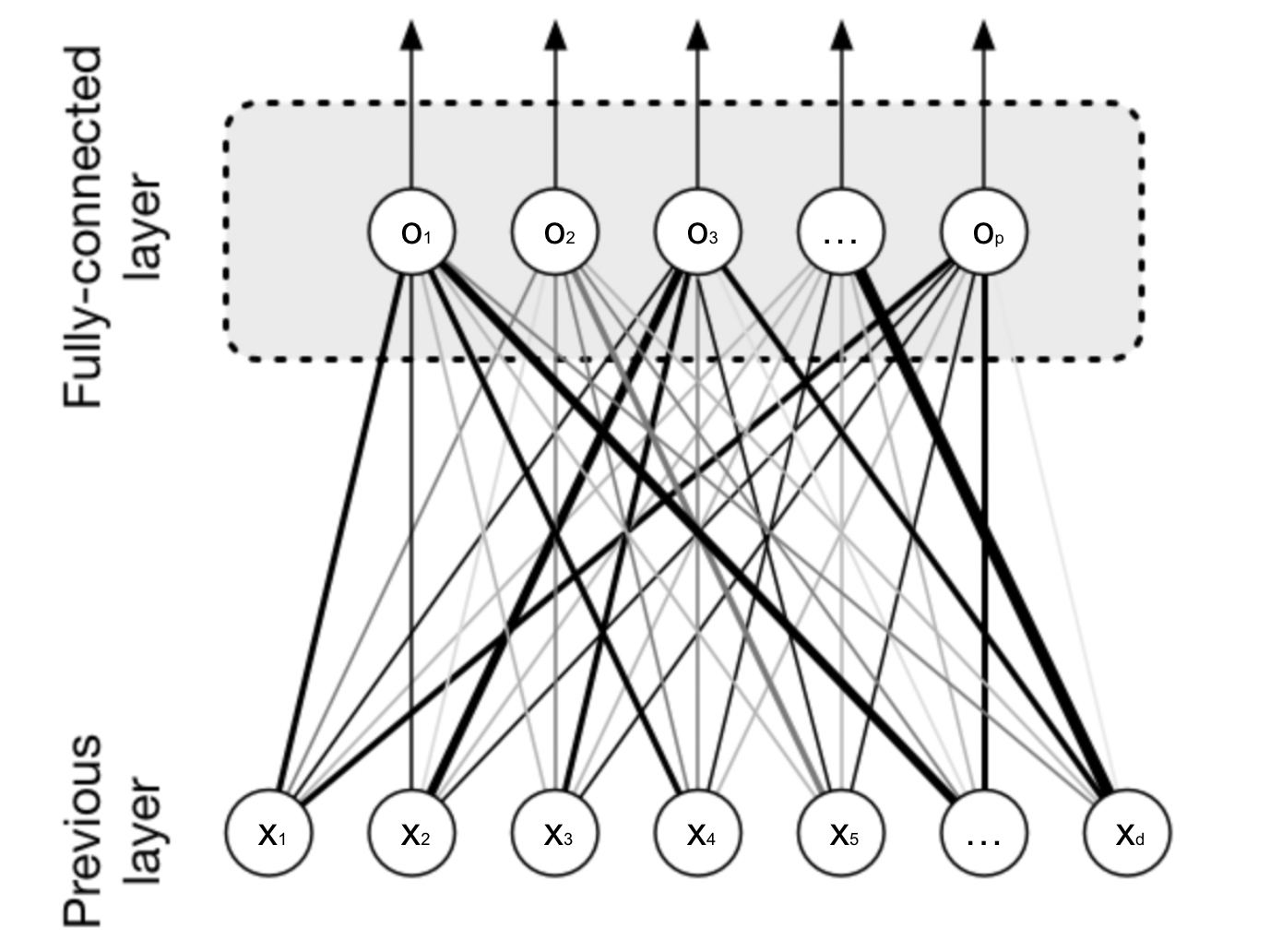
\[ h_{i} = \sigma{\sum^{P}_{j=i}}W_{i,j}x_{j} \]
Fully connected layer는 다층 신경망의 경우 각 성분의 가중치 행들이 i 번째 위치마다 필요했다. 또한 $h_{i}$ 를 계산할 때 $W_{i}$가 필요했고, i 가 바뀌게 되면 가중치 행렬의 행도 바뀌어서 구조가 커지게되고, 실제로 학습을 시켜야하는 parameter의 숫자도 굉장히 많이 커졌다.
Convolution은 kernel이라는 고정된 가중치 행렬을 사용하고 고정된 kernel을 입력 벡터 상에서 움직여가면서 선형 모델과 합성함수가 적용되는 구조이다.
kernel의 등장 배경

실험을 통해 사람의 뇌가 이미지를 인식할 때, 각 작은 형태에 따라 다른 부위의 뉴런이 자극된다는 것을 알 수 있었다.
이걸 기반으로 사람들이 복잡한 사진을 봤을 때 한번에 보는 것이 아니라 작은 부위별로 보는 것이 아닐까 라는 추론을 하게 되었다. 즉 간단한 (선의 두께 등) 것들을 담당하는 뉴런들이 따로 있다라는 결론이다.

또한 뉴런들이 계층구조를 이루어 얕은 구조에 있는 뉴런들은 단순한 상황, 즉 빛이 있는가 없는가와 같이 간단한 정보에 활성되고, 깊어질 수록 선이 움직이는가, rotate하는가, 선이 이어지는가 끝나는가와 같은 더 고차원 적인 정보들을 뉴런들이 담당하고 있다는 사실을 발견하게 되었다. 즉, 각 해당의 neuron들은 하단의 간단한 정보들을 모아서 취합해서 더 복잡한 정보, 즉 고차원 적인 정보를 알아내는 것이 아닐까라는 것을 발견하게 되었다. 더 나아가면, 고양이, 사람 얼굴을 알아 맞추는 것도 하단의 뉴런들이 취한 정보의 결합을 통해서 만들어낸다는 것이다.
MLP는 spatial한 정보 즉, 서로 위치에서 가까웠던 pixel의 정보를 보존하지 못한다. 이에 따라 spatial information은 유지를 시키기 위해서 이미지는 그대로 두고, filter인 kernel을 씌운다.
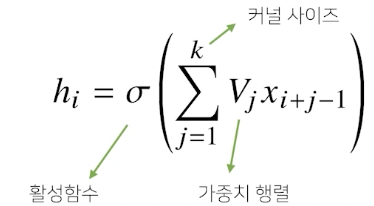
입력벡터 x 를 모두 이용하는 것이 아니라, kernel 사이즈에 대응되는 만큼 추출을 한다.
즉, 입력 벡터상에서 kernel사이즈만큼 움직여가며 계산한다.
가중치 행렬이 i 번째 위치에 따라서 따로 존재하지 않고, kernel 사이즈가 고정이라 파라미터 사이즈를 굉장히 많이 줄일 수 있다.
Convolution 연산의 수학적 의미는 정의역이 연속인 공간에서 적분을 사용해서 정의할 수 있고, 이산 공간에서는 급수(summation)로 정의할 수 있다.
수식 이해
연속형
$$ [f \ast g](x) = \int_{\mathbb{R}^{d}} f(z)g(x-z)dz = \int_{\mathbb{R}^{d}} f(x-z)g(z)dz = [g \ast f](x) $$
이산형
$$ [f \ast g](i) = \sum_{a \in \mathbb{Z}^{d}} f(a)g(i-a)= \sum_{a \in \mathbb{Z}^{d}}f(i-a)g(a)= [g \ast f](i) $$
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=sw4r&logNo=220904800372
[Convolution의 완벽한 이해] Convolutional Neural Network (CNN) - 이론편 1/2
CNN은 딥러닝 알고리즘의 하나로 많이들 아실 것 같은데요 거기에 들어가는 기본적인 알고리즘과 수학적...
blog.naver.com

$\ast$는 사칙연산이 아닌 연산자로, $\times, +$를 결합한 것 처럼 수행된다.
두 신호 f,g 를 합쳐서 새로운 신호를 만드는 수학적 방법
커널을 이용해서 국소적으로 정보를 증폭 또는 감소시켜서 정보를 추출 또는 필터링 하는 것.
연속형
$$ [f \ast g](x)=\int_{\mathbb{R}^{d}}f(z)g(x\text{+}z)dz=\int_{\mathbb{R}^{d}} f(x\text{+}z)g(z)dz =[g \ast f](x) $$
이산형
$$[f\ast g](i)=\sum_{a\in\mathbb{Z}^{d}}f(a)g(i\text{+}a)=\sum_{a \in\mathbb{Z}^{d}}f(i\text{+}a)g(a)=[g\ast f](i)$$
위 첨부된 블로그 글에서 확인 할 수 있듯이, CNN 에서 사용되는 연산은 convolution이 아니라, cross-correlation이다. 단지 부를 때 convolution이라 부르는 것.
https://brunch.co.kr/@chris-song/24
컨볼루션(Convolution) 이해하기
Understanding Convolutions - Chris Olah | 이 글은 colah.github.io 의 블로그의 글을 저작자 Chris Olah의 허락을 받고 번역한 글입니다. 의 블로그의 글을 저작자 Chris Olah의 허락을 받고 번역한 글입니다. http://co
brunch.co.kr
컨볼루션(Convolution) 정의를 쉽게 이해해보자 - DKMIN
컨볼루션(Convolution) 정의에 대해 글을 썼습니다. 검색을 하다보니 대학시절에 이거 공부하느라 삽질했던 기억이 떠올라 주먹 감자가 저절로 쥐어졌습니다. 매우 빡친 상태에서 글을 작성해서 고
dkeemin.com
위 첨부된 글들을 모두 읽으면 전체적으로 convolution이 이해된다.
영상처리에서 convolution

커널의 종류에 따라 영상이 바뀐다.
Convolution 연산은 1차원 뿐만 아니라 다양한 차원에서 계산이 가능하다.



흑백 영상: 2D, 컬러 영상: 3D
convolution 연산의 핵심은 커널이 i,j,k 등 위치에 따라 바뀌지 않는다는 것이다.
2차원 커널
2차원 Convolution 연산은 입력 행렬에 해당하는 데이터에서 kernel을 x,y 방향으로 한칸씩 움직이며 적용한다.

입력 크기를 ($H,W$), 커널 크기를 ($K_{H}, K_{W}$), 출력 크기를 ($O_{H}, O_{W}$)라 하면 출력 크기는 다음과 같이 계산합니다.
\[ O_{H} = H-K_{H}+1 \]
\[ O_{W} = W-K_{W}+1 \]
ex) 28 $\times$ 28 입력을 3 $\times$ 3 커널로 2D-Conv 연산을 하면 26 $\times$ 26 이다.
3차원 커널
실제로 영상 데이터는 3차원 이상인 경우가 많다. R,G,B 만 추가되어도 3차원 입력 데이터를 다루게 된다.
채널이 여러개인 2차원, 즉 3차원 입력의 경우 2D-Conv를 사용한다. 다만, 채널 개수만큼 kernel을 만들어 적용한다.


커널의 채널 개수와 입력의 채널 개수를 같게 설정하기 때문에, Conv 연산 후 출력에 해당하는 tensor 3차원의 차원은 1이 된다.
출력이 여러개의 채널을 갖게 하려면, 커널의 개수를 여러개 만들면 된다.
원하는 출력의 채널 개수만큼 커널의 개수를 만들어주면 된다.

Convolution 연산의 역전파

딥러닝 - 초보자를 위한 컨볼루셔널 네트워크를 이용한 이미지 인식의 이해
딥러닝 - 컨볼루셔널 네트워크를 이용한 이미지 인식의 개념 조대협 (http://bcho.tistory.com) 이번 글에서는 딥러닝 중에서 이미지 인식에 많이 사용되는 컨볼루셔널 뉴럴 네트워크 (Convolutional neural n
bcho.tistory.com
추가설명
'AI > CV' 카테고리의 다른 글
| CNN Visualization (0) | 2022.03.11 |
|---|---|
| Semantic segmentation (0) | 2022.03.10 |
| semantic segmentation, Detection (0) | 2022.02.08 |
| Convolution network model 소개 (ILSVRC 모델) (0) | 2022.02.08 |
| CNN 간단 정리 2 (0) | 2022.02.08 |




