머신러닝 정리 4.5(7) - 특이값 분해 (SVD)

본 글은 https://angeloyeo.github.io/2019/08/01/SVD.html

특이값 분해(SVD) - 공돌이의 수학정리노트

 내용을 이해하되, 중간중간 기본적 개념을 조금 더 추가한 글입니다. 

 

특이값 분해(Singular Value Decomposition, SVD)는 임의로 $m /times n$ 차원의 행렬 $A$에 대하여 다음과 같이 행렬을 분해할 수 있다는 '행렬 분해' 방법 중 하나이다. 

 

차원 축소 기법 PCA 에 대해 살펴보았었는데, SVD 도 차원 축소 기법 중 하나이다. (차원 추출)

추천 시스템 관련 글에서 SVD 즉 특이값 분해를 다뤘었기에 그 글만 참고해도 좋다. 

 

$$A = U \Sigma V^T$$

 

A 라는 행렬을 다음과 같이 $U, V^T$ 로 분해 가능 

 

 

---

 

orthogonal: 직교

orthogonal matrix는 모든 column vector가 자기 자신을 제외한 나머지 모든 column vector들과 직교이면서 크기가 1인 단위 벡터들로 구성된 행렬 

 

벡터가 서로 직교할 때, 우리는 직교벡터라 한다. 이 때 각 벡터의 내적은 0 이다. 

정규직교(orthonormal)벡터: 두 벡터가 직교벡터이면서 각 벡터의 길이는 1인 방향성분만을 나타내는 벡터 

 

단위 벡터는 자기 자신과 곱하면 즉 내적하면 결과값이 1이다. (단위벡터의 norm이 1이기에 당연한 결과이다.)

 

자기 사진을 제외한 나머지 모든 벡터들과는 직교한다. 

즉, 자기 자신을 제외한 나머지 벡터들과의 내적 결과가 0이 된다. 

 

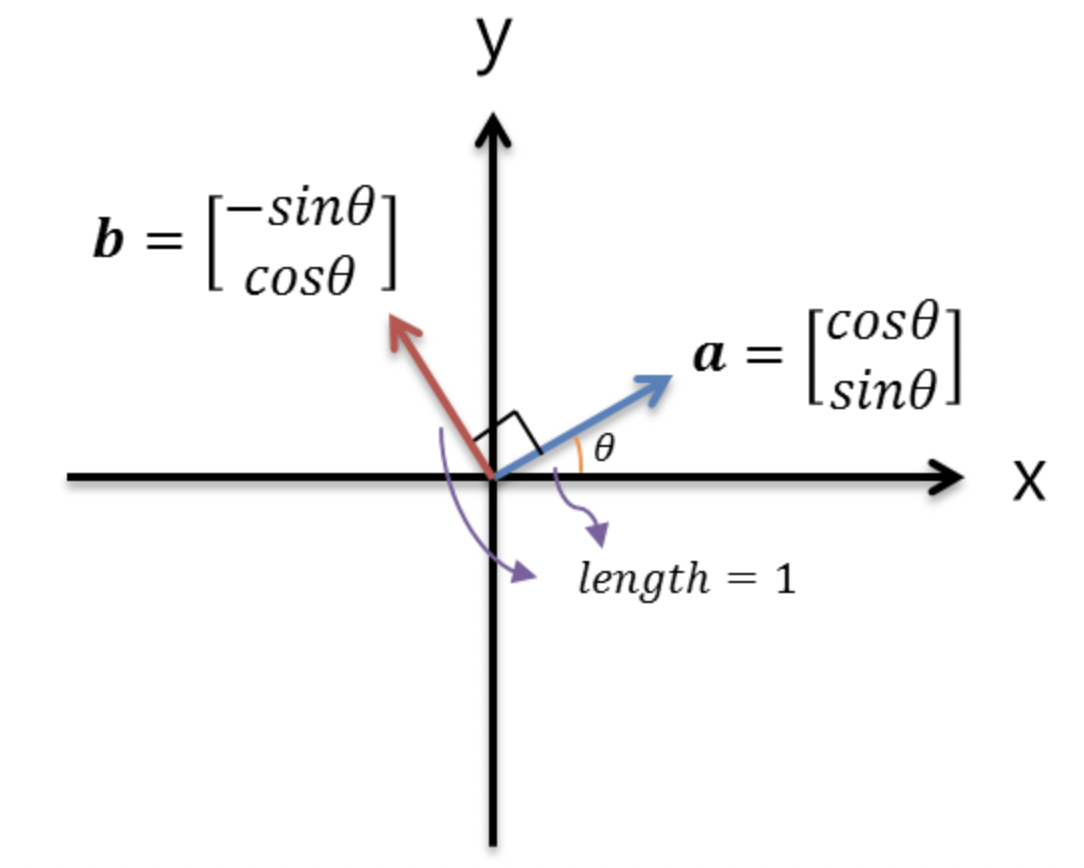
sin과 cos 으로 이루어진 벡터를 나타낸다. 이들 벡터 a,b의 길이는 각각 1이며 둘 사이의 각도는 90도 이다. 두 벡터가 직교하며 각 벡터의 길이는 1로써 방향성분만 나타내므로 이들은 정규직교벡터이다. 

 

이러한 정규직교벡터들은 행렬의 column vector에 삽입하면 직교행렬이 된다. 

즉 Q 를 직교행렬이라고 했을 때 orthonormal vector들의 Q의 정규직교기저가 되는 것이다. 아래의 그림 같이 말이다. 

이러한 정규직교기저는 선형대수의 행렬 계산에 있어 좋은 결과를 보여준다. 

 

$q_1 ... q_n$: 각각은 orthnormal vector 

 

즉, $q_i$ 는 자기 자신을 제외한 나머지 벡터들과 직교하다. 

 

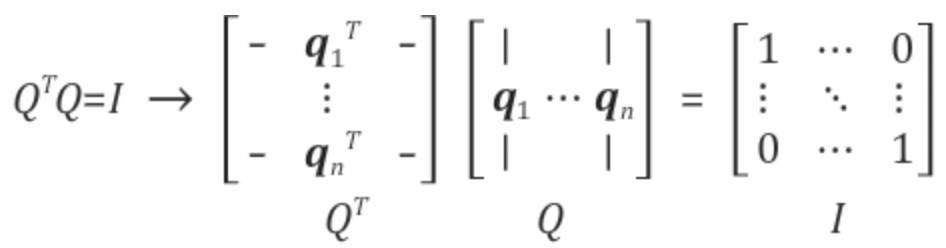
Q transpose와 Q 를 곱하면 Identity matrix가 나타난다. 

(직교 벡터끼리의 곱은 0이고, 자기자신의 곱은 단위벡터의 내적이기에 1)

 

정리하자면 정규직교 벡터를 column으로 갖는 직교행렬을 배웠다. 정규 네임이 orthonormal matrix 여야 할 것 같지만, orthogonoal matrix 라 한다. 

 

직교행렬의 특성 

 

1. 정방행렬인 직교행렬은 transpose 가 역행렬과 동일하다. 

 

단위 행렬의 각 column vector는 자기 자신을 제외한 나머지 벡터와 90도의 각도를 이루면서 크기가 1이어야 한다. 이를 시각화하면 아래와 같다. 

 

 

 

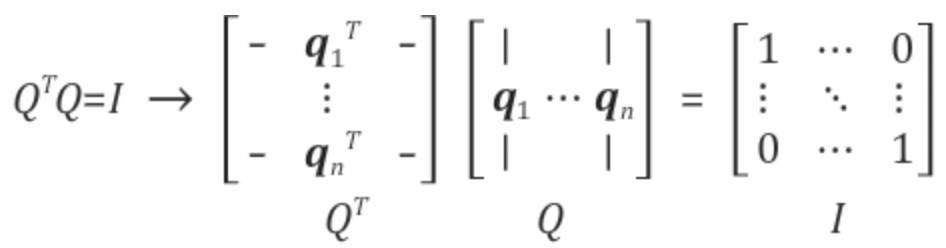
아까 살펴보았듯이, 정방행렬인 상황에서는 자기 자신과 곱해진 경우는 1, 이외에는 직교로 0이 되므로 단위행렬을 만들어내고, 이는 결국 역행렬의 특성과 동일하다. 

 

2. 모든 colum이 직교 벡터를 가지나 각 벡터의 크기가 1이 아닐 때 직교 행렬을 만드는법 

 

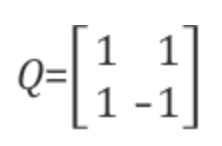
벡터의 크기로 행렬 원소 전체를 나누어주면 된다. 

 

여기서는 column $q_1, q_2$의 크기가 같아서 동일하게 나눠줬지만, 다를 경우에는 각자의 크기로 나눠주면 된다. 

 

직교 행렬을 만드는 방법으로 그람-슈미트 과정이 있다. 본 내용은 추후 다시 다룬다. 

 

직교 행렬 사용의 장점 

추후 읽어보자 

https://twlab.tistory.com/37

https://twlab.tistory.com/34

 

 

단위 벡터: 

크기가 1인 방향만이 의미를 갖는 벡터 

 

 

※Diagonal Matrix 

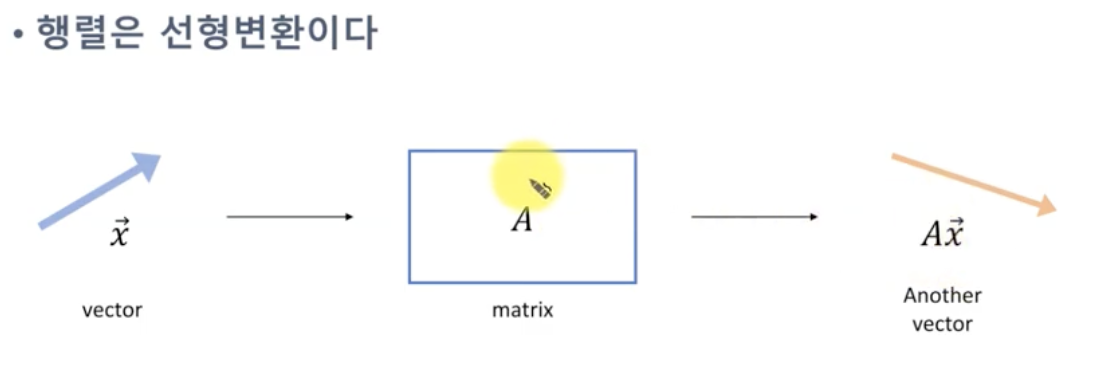
대각 행렬 : 행렬은 선형 변환이다. 이 중, diagonal matrix 는 벡터의 크기를 조정한다. 

scaling factor를 0으로 하면 차원을 축소하는 것도 가능하다. 

 

 

---

 

 

SVD의 기하학적 의미 

 

직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만, 여전히 직교할 수 있게 만드는 그 직교 벡터 집합은 무엇이고, 변형 후의 결과는 무엇인가? 

 

이 말의 뜻이 이해가 잘 안간다면 

https://angeloyeo.github.io/2019/08/01/SVD.html

특이값 분해(SVD) - 공돌이의 수학정리노트

위 글에서 직접 시각화 툴을 선형 변환하며 직교가 유지되는 경우를 살펴보면 이해에 도움이 된다. 

 

 

직교하는 벡터 x, y 가 있다고 할 때, 두 벡터가 선형 변환 한 결과 Ax, Ay 도 여전히 직교하는지 살펴보자. 

위 경우에는 Ax, Ay가 직교하지 않는다. 

 

하지만 위 그림과 같이 잘 조정하다보면 어떤 경우에는 x,y 도 직교하고 Ax, Ay 도 직교한다. 

 

이 경우 우리는 벡터 x,y 를 가지고 singular vector decomposion 을 했다고 할 수 있다. 

 

기하학적 의미를 다시 살펴보자. 

 

직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만, 여전히 직교할 수 있게 만드는 그 직교 벡터 집합은 무엇이고, 변형 후의 결과는 무엇인가? 

 

벡터 집합이란, 결국 column 벡터를 갖는 행렬을 말한다.

 

결국 정리하자면, 

직교하는 벡터 집합: $V$

 

선형 변환: $A$

 

크기는 변하지만 여전히 직교할 수 있게 만드는 직교 벡터 집합: $\Sigma$

 

변경 후의 결과: $U$ 

 

이다. 

 

$U = AV \cdot \Sigma$

$U \Sigma^T = AV$

$U \Sigma^T V^T = A$

 

$A = U \Sigma V^T$

 

(선형변환을 한 직교하는 벡터 집합(행렬)에 orthogonal한 벡터 집합을 곱해도 여전히 직교하는 벡터 집합이 존재한다)

 

U, V 계산법은 eigenvalue decomposition 이라는 기법을 이용해야 한다. 추후 정리하자. 

 

위 결과물을 보면, sigma가 마치 각 항에 weight 의 역할을 하는 것을 알 수 있다. 

즉 이 scaling fator 가 A가 가지고 있는 matrix 의 정보량을 결정해준다. 

 

즉, SVD 방법을 통해 A 라는 임의의 행렬을 여러개의 A 행렬과 동일한 크기를 갖는 여러개의 행렬로 분해해서 생각할 수 있는데, 분해된 각 행렬의 원소의 값의 크기는 sigma 의 값의 크기에 의해 결정된다. 

 

다시말해 SVD를 이용해 임의의 행렬 A 를 정보량에 따라 여러 layer로 쪼개서 생각할 수 있게 한다. 

 

 

 

특이값 분해의 활용

특이값 분해는 분해되는 과정보다는 분해된 행렬을 다시 조합하는 과정에서 그 응용력이 빛을 발한다. 

 

기존의 $\Sigma, U, V^T$ 로 분해되어 있던 A 행렬을 특이값 p개만을 이용해 $A^'$ 라는 행렬로 부분 복원 할 수 있다. 위에서 말했던 것 특이값의 크기에 따라 A 의 정보량이 결정되기 때문에 값이 큰 몇개의 특이값만을 가지고도 충분히 유용한 정보를 유지할 수 있다. 

즉, 이를 통해 차원을 축소할 수 있다.

 

정보를 다 반영 안해도 상당한 정보를 얻을 수 있다. 

 

 

(입출력의 차원이 다른 변환의 경우에도 사용 가능하다.)

아래 블로그 참고 

https://angeloyeo.github.io/2019/08/01/SVD.html

특이값 분해(SVD) - 공돌이의 수학정리노트

 

마지막으로 해당 개념은 추천시스템에서도 활용된다. 

 

 

User item 정보를 User, Item 그리고 차원을 맞춰주며 동시에 중요도에 따라 scaling 하는 $\Sigma$ 행렬로 분해할 수 있다. 

 

여기서 User, Item 의 행렬은 orthogonal 행렬이다. $\Sigma$ 는 diagonal matrix 이다. 

 

분석 후, 중요도에 따라 K의 factor만을 선정하여 $\hat{R}$을 복원한다. 

 

계산방법은 아래의 블로그 내용을 참고하자. 

https://ys-cs17.tistory.com/52

SVD의 기본 이론과 이해 및 활용